Question

How do you solve the system of inequalities $y<3x-5$ and $y>-4x-7$ .

Answer 1

Hint: Now to solve the inequalities we will find the corresponding equality and hence plot the line of the equality. Now check if the origin satisfies the inequality. If it satisfies the inequality then the origin side is the solution set or in other case the opposite side is the solution set. Hence we will find the solution sets on graph and then the solution to the inequalities is the intersection of both solution sets.

Complete step by step solution:
Now we are given with two linear inequalities. To solve the linear equations we will first graph the both inequalities and then find the intersection area of the two inequalities.
First let us consider $y<3x-5$ .
The corresponding linear equation to the inequality is $y=3x-5$
Now let us plot the line $y=3x-5$ .
Now on substituting the value of x we will find the corresponding values of y and hence find the solution of the equation.
Now on substituting x = 0 we get y = - 5.
Similarly on substituting x = 1 we get y = -2.
Hence we have the point (0, -5) and (1, -2) lies on the equation of the given line.
Let us plot the line by plotting the points and drawing a line passing through the points.

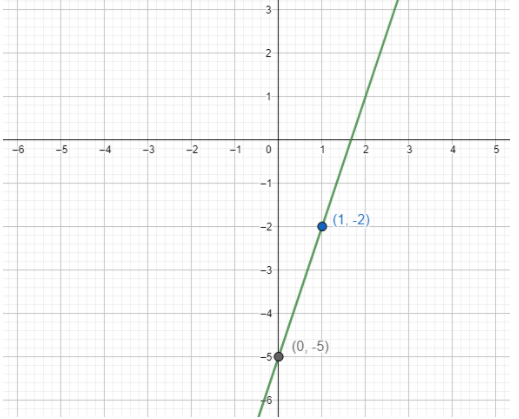
Now consider the inequality $y<3x-5$ Now we can see that the point (0, 0) does not satisfy the equation. Hence the area of the inequality is on the non origin side.
Hence the graph of inequality is,

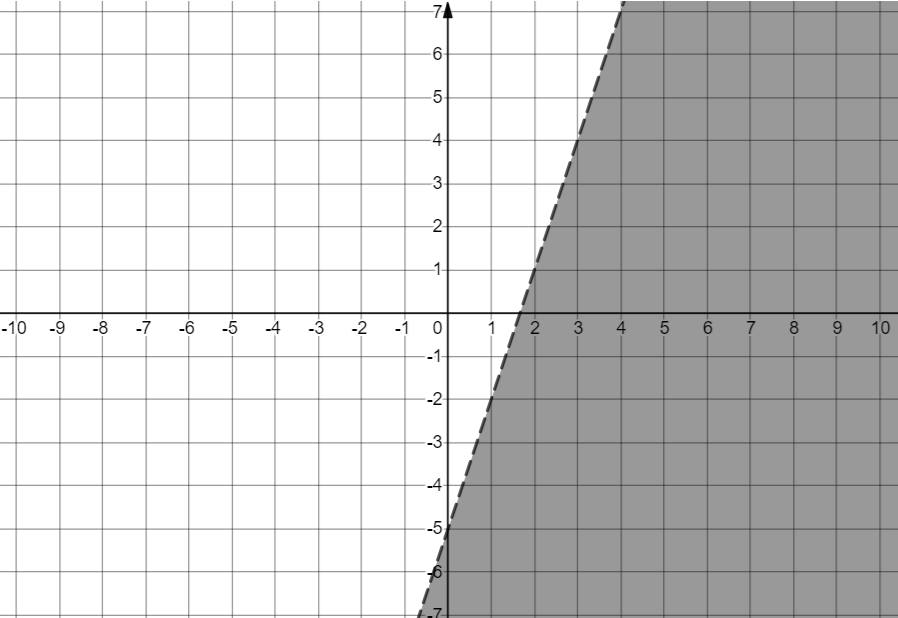
Now similarly consider the equation $y>-4x-7$
The corresponding equation is $y=-4x-7$ .
Now on substituting the value of x = 0 we get y = - 7.
Now on substituting x = - 2 we get y = 1
Hence the points (0, -7) and (-2, 1) lie on the equation.
Hence we will plot the points and draw a line passing through the points.

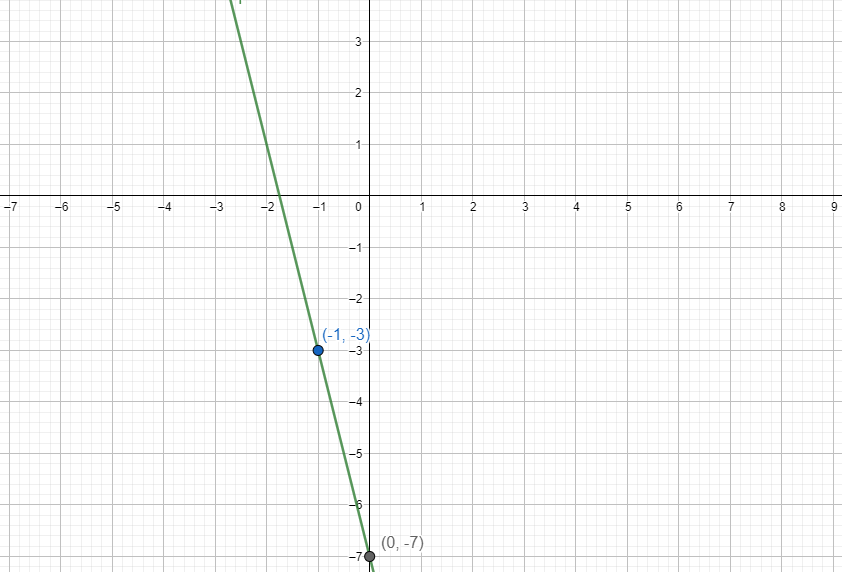
Now consider the inequality $y>-4x-7$
Now we can see that the point (0, 0) satisfies the inequality. Hence the area required is the origin side area of the line.

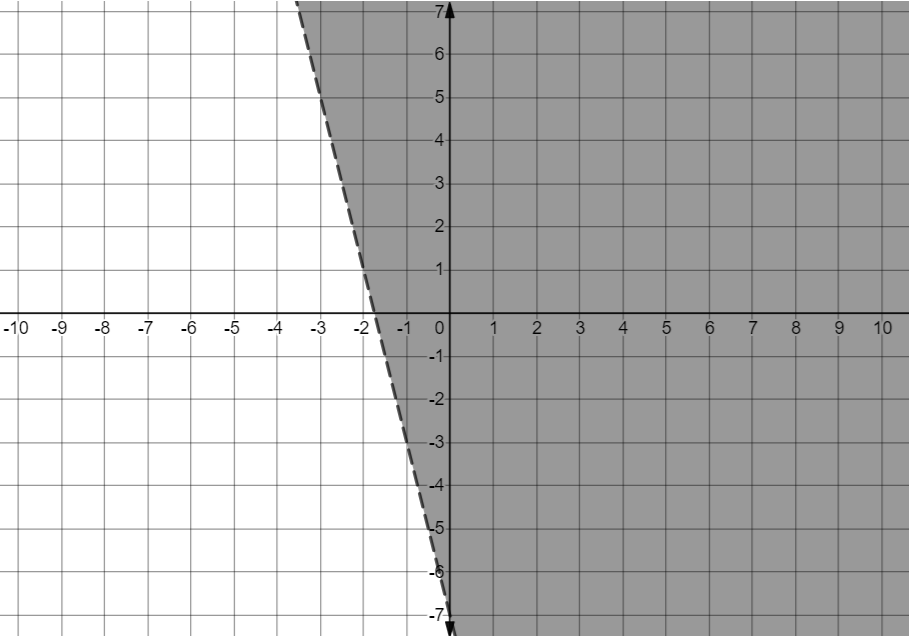
Now the solution of the two simultaneous inequalities is the intersection of both areas.
Hence we get,

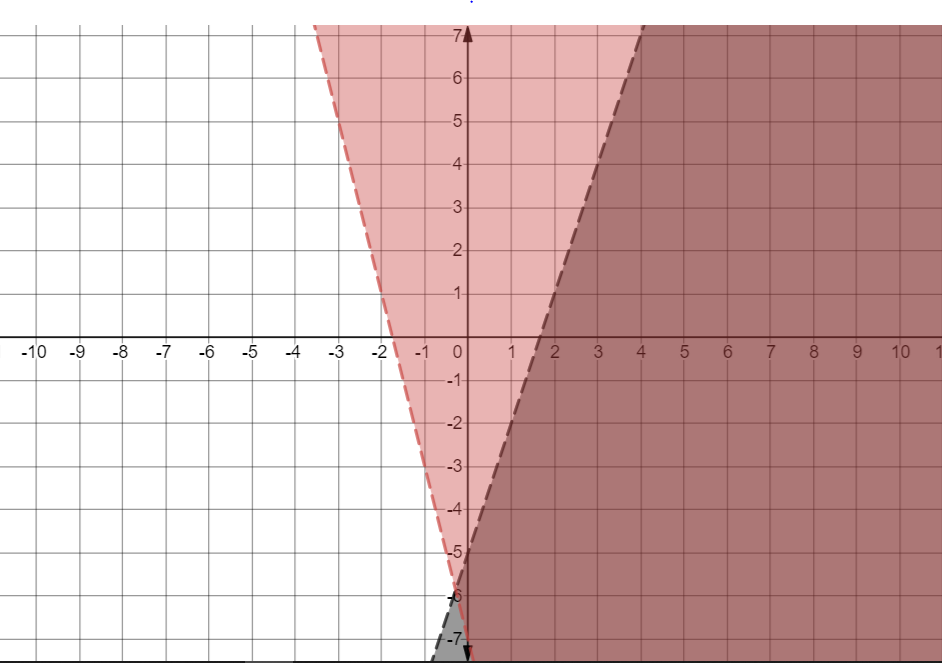
The area in dark pink is the required area.

Note: Now note that while plotting inequality we will first plot the corresponding equality. Now take a point on any side of the line and check if it satisfies the inequality. If the point satisfies the inequality then the point is in the solution set of the inequality and hence that side of the line is the whole solution set. If it does not satisfy the inequality then the opposite side is the solution set. Now we can take any point to check this but for simplicity it is better to take origin.