
How do you solve the system of equations $x+3y=-7$ and $-x-3y=1$?
Answer
552.3k+ views
Hint: The given two equations must first be written in the form of $ax+by+c=0$ by taking the constant terms from both on the LHS. Then, we need to calculate the ratios of the coefficients of x, y and that of the constant terms. If the ratio comes out as $\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{{{c}_{1}}}{{{c}_{2}}}$, then the system will have infinite solutions, if the ratio comes as $\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}\ne \dfrac{{{c}_{1}}}{{{c}_{2}}}$, then the system will have no solution, and if the ratio comes as $\dfrac{{{a}_{1}}}{{{a}_{2}}}\ne \dfrac{{{b}_{1}}}{{{b}_{2}}}$, then the system will have a unique solution.
Complete step by step solution:
Considering the first equation, we have
$\Rightarrow x+3y=-7$
Adding $7$ both the sides, we get
$\Rightarrow x+3y+7=0.........\left( i \right)$
And the second equation is
$\Rightarrow ~-x-3y=1$
Subtracting $1$ from both the sides, we get
$\Rightarrow -x-3y-1=0.........\left( ii \right)$
From the equation (i) we note the coefficient of x as ${{a}_{1}}=1$, the coefficient of y as ${{b}_{1}}=3$, and the constant term as ${{c}_{1}}=7$.
Similarly, from the equation (ii) we note ${{a}_{2}}=-1$, ${{b}_{2}}=-3$, and ${{c}_{2}}=-1$.
Now, the ratio of the coefficients of x is
\[\begin{align}
& \Rightarrow \dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{1}{-1} \\
& \Rightarrow \dfrac{{{a}_{1}}}{{{a}_{2}}}=-1.......\left( iii \right) \\
\end{align}\]
The ratio of the coefficients of y is
\[\begin{align}
& \Rightarrow \dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{3}{-3} \\
& \Rightarrow \dfrac{{{b}_{1}}}{{{b}_{2}}}=-1.......\left( iv \right) \\
\end{align}\]
And the ratio of the constant terms is
\[\begin{align}
& \Rightarrow \dfrac{{{c}_{1}}}{{{c}_{2}}}=\dfrac{7}{-1} \\
& \Rightarrow \dfrac{{{c}_{1}}}{{{c}_{2}}}=-7.......\left( v \right) \\
\end{align}\]
From (iii), (iv) and (v) we can say that
$\Rightarrow \dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}\ne \dfrac{{{c}_{1}}}{{{c}_{2}}}$
We know that this is the condition for the inconsistency.
Therefore, the given system of the equations is inconsistent, and hence it has no solution.
Note: We can also solve the above question graphically. The two equations given in the above question can be considered as the equations of two straight lines. Their plots are shown in the below figure.
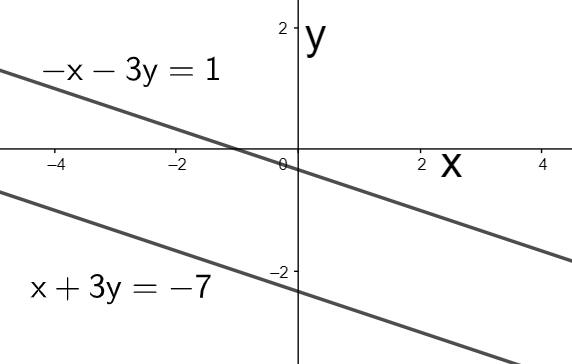
As we can clearly see from the above figure that the two straight lines represented by the given equations are parallel and are separated by a distance. We know that the parallel lines never intersect each other. Therefore, the given two equations will have no point common and hence, the given system will have no solution.
Complete step by step solution:
Considering the first equation, we have
$\Rightarrow x+3y=-7$
Adding $7$ both the sides, we get
$\Rightarrow x+3y+7=0.........\left( i \right)$
And the second equation is
$\Rightarrow ~-x-3y=1$
Subtracting $1$ from both the sides, we get
$\Rightarrow -x-3y-1=0.........\left( ii \right)$
From the equation (i) we note the coefficient of x as ${{a}_{1}}=1$, the coefficient of y as ${{b}_{1}}=3$, and the constant term as ${{c}_{1}}=7$.
Similarly, from the equation (ii) we note ${{a}_{2}}=-1$, ${{b}_{2}}=-3$, and ${{c}_{2}}=-1$.
Now, the ratio of the coefficients of x is
\[\begin{align}
& \Rightarrow \dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{1}{-1} \\
& \Rightarrow \dfrac{{{a}_{1}}}{{{a}_{2}}}=-1.......\left( iii \right) \\
\end{align}\]
The ratio of the coefficients of y is
\[\begin{align}
& \Rightarrow \dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{3}{-3} \\
& \Rightarrow \dfrac{{{b}_{1}}}{{{b}_{2}}}=-1.......\left( iv \right) \\
\end{align}\]
And the ratio of the constant terms is
\[\begin{align}
& \Rightarrow \dfrac{{{c}_{1}}}{{{c}_{2}}}=\dfrac{7}{-1} \\
& \Rightarrow \dfrac{{{c}_{1}}}{{{c}_{2}}}=-7.......\left( v \right) \\
\end{align}\]
From (iii), (iv) and (v) we can say that
$\Rightarrow \dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}\ne \dfrac{{{c}_{1}}}{{{c}_{2}}}$
We know that this is the condition for the inconsistency.
Therefore, the given system of the equations is inconsistent, and hence it has no solution.
Note: We can also solve the above question graphically. The two equations given in the above question can be considered as the equations of two straight lines. Their plots are shown in the below figure.
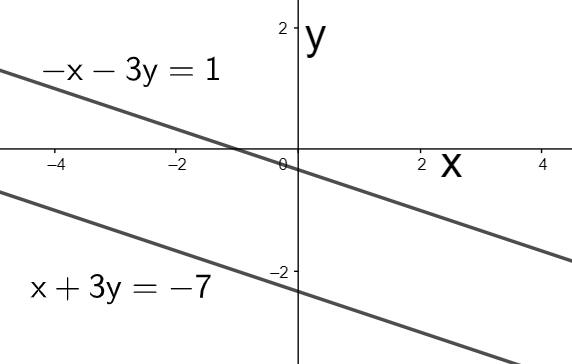
As we can clearly see from the above figure that the two straight lines represented by the given equations are parallel and are separated by a distance. We know that the parallel lines never intersect each other. Therefore, the given two equations will have no point common and hence, the given system will have no solution.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which places in India experience sunrise first and class 9 social science CBSE

Who is eligible for RTE class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE





