Question

How do you solve the system of equations \[8x - y = 29\] and \[2x + y = 11\] by graphing?

Answer 1

Hint: As there are two equations involved, in which we need to solve for x and y. To solve the given simultaneous equation, combine all the like terms or by using any of the elementary arithmetic functions i.e., addition, subtraction, multiplication and division hence simplify the terms to get the value of \[x\] also the value of \[y\] and plot the graph.

Complete step-by-step answer:
Let us write the given equation
 \[8x - y = 29\] …………………………. 1
 \[2x + y = 11\] ..………………………… 2
We need to plot the straight lines: \[8x - y = 29\] and \[2x + y = 11\] by solving the value of x and y. Hence, let us find the values of x and y then graph the solution.
The standard form of simultaneous equation is
 \[Ax + By = C\]
Equation 2 can be written in terms of \[y\] to get the value of \[x\] that is
 \[2x + y = 11\]
 \[ \Rightarrow \] \[y = 11 - 2x\] …………………………… 3
Hence, substitute the value of \[y\] in equation 1 as
 \[8x - y = 29\]
 \[ \Rightarrow \] \[8x - \left( {11 - 2x} \right) = 29\]
 \[ \Rightarrow \] \[8x - 11 + 2x = 29\]
After substituting the y term, simplify the obtained equation
 \[10x - 11 = 29\]
Which implies that
 \[10x = 29 + 11\]
 \[10x = 40\]
Therefore, the value of \[x\] after simplifying the terms we get
 \[x = \dfrac{{40}}{{10}}\]
 \[x = 4\]
As we got the value of \[x\] , substitute the value of \[x\] as 4 in equation 3 we get,
 \[y = 11 - 2x\]
 \[y = 11 - 2\left( 4 \right)\]
 \[y = 11 - 8\]
 \[y = 3\]
Therefore, the value of \[y\] is 3.
Hence the values of \[x\] and \[y\] are
 \[x = 4\] and \[y = 3\]

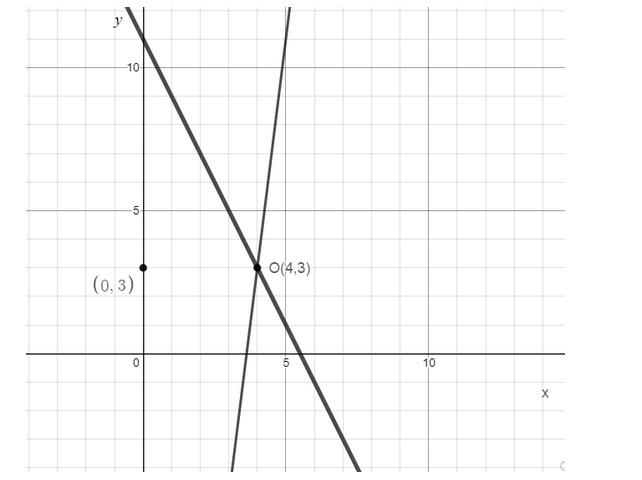
Note: Simultaneous equations are a set of two or more equations, each containing two or more variables whose values can simultaneously satisfy both or all the equations in the set, the number of variables being equal to or less than the number of equations in the set.
To graph the solution we have considered both x and y values by straight lines. We know that Simultaneous equations are two equations, each with the same two unknowns and are simultaneous because they are solved together, hence the key point to solve these kinds of equations we need to combine all the terms and then simplify the terms to get the value of \[x\] also the value of \[y\] .