Question

How do you solve the system of equations $3x+3y=9$ and $5x-3y=7$ ?

Answer 1

Hint: We have been given two linear equations in two variables, x and y, which must be solved simultaneously in order to obtain their solution. The solution is the point of intersection of the two lines which can be easily determined after sketching the graph of both lines on the same cartesian plane and marking the point where the two lines meet.

Complete step by step solution:
We will put the values of x and y equal to zero one by one to find two simple points one of which will have its x-coordinate equal to zero and the other one would have its y-coordinate equal to zero.
We shall first find the points lying on the line whose equation is given by, $3x+3y=9$.
Putting $x=0$ in the equation, we get
$3\left( 0 \right)+3y=9$
$\Rightarrow 3y=9$
Now, we shall take divide both sides by 3 to find y:
$\begin{align}
  & \Rightarrow y=\dfrac{9}{3} \\
 & \Rightarrow y=3 \\
\end{align}$
Therefore, we get the point as (0, 3).
Putting $y=0$ in the equation, we get
$3x+3\left( 0 \right)=9$
$\Rightarrow 3x=9$
Now, we shall divide both sides by 3 to find x:
$\Rightarrow x=\dfrac{9}{3}$
$\therefore x=3$
Therefore, we get the point as (3,0)
Hence, the points are $\left( 0,3 \right)$and $\left( 3,0 \right)$. ……………………….. (1)
We shall now find the points on the second equation given as, $5x-3y=7$.
Putting $x=0$ in the equation, we get
$\begin{align}
  & 5\left( 0 \right)-3y=7 \\
 & \Rightarrow -3y=7 \\
\end{align}$
Dividing both sides by -3, we get
$\Rightarrow y=-\dfrac{7}{3}$
Therefore, we get the point as $\left( 0,-\dfrac{7}{3} \right)$.
Putting $y=0$ in the equation, we get
$\begin{align}
  & 5x-3\left( 0 \right)=7 \\
 & \Rightarrow 5x=7 \\
\end{align}$
Dividing both sides by 5, we get
$\Rightarrow x=\dfrac{7}{5}$
Therefore, we get the point as $\left( \dfrac{7}{5},0 \right)$.
Hence, the points are $\left( 0,-\dfrac{7}{3} \right)$and $\left( \dfrac{7}{5},0 \right)$. ……………………… (2)
From (1) and (2), we get the graph as:

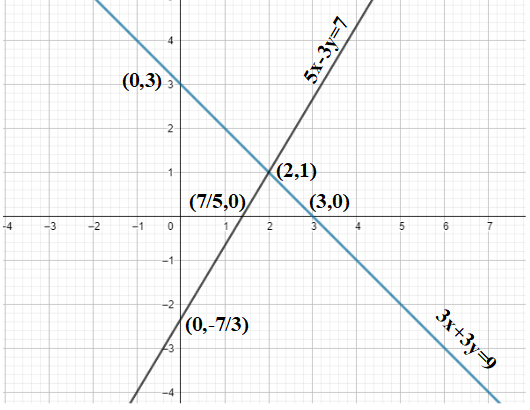
Therefore, the solution of the given system of equations is (2,1) as the two lines are intersecting at this point.

Note: While sketching any graph, the two points should always be taken such that the x or y coordinates are zero in them as it makes the calculations easier. While plotting the graph, the points must be marked with precision. One possible mistake we could have done was marking (-3,0) instead of (3,0).