Question

How do you solve the system by graphing \[-2x-y=-2,4x+y=4\]?

Answer 1

Hint: Draw the graph of the two given equations. To draw the graph of a straight line, we need at least two points. So, choose one of the equations and substitute x = 0, determine y, then substitute y = 0, determine x. Now, apply the same process for the second equation. Plot the graph of the two equations using the points obtained. Check the point of intersection to get the answer.

Complete step-by-step answer:
Let us assume the two equations as: -
\[\Rightarrow -2x-y=-2\] - (1)
\[\Rightarrow 4x+y=4\] - (2)
Now, let us consider equation (1), we have,
\[\Rightarrow -2x-y=-2\]
Substituting x = 0, we get,
\[\begin{align}
  & \Rightarrow -y=-2 \\
 & \Rightarrow y=2 \\
\end{align}\]
Substituting y = 0, we get,
\[\begin{align}
  & \Rightarrow -2x=-2 \\
 & \Rightarrow x=+1 \\
\end{align}\]
Therefore, the two points are: - A (0, 2) and B (1, 0).
Now, let us consider equation (2), we have,
\[\Rightarrow 4x+y=4\]
Substituting x = 0, we get,
\[\Rightarrow y=4\]
Substituting y = 0, we get,
\[\begin{align}
  & \Rightarrow 4x=4 \\
 & \Rightarrow x=1 \\
\end{align}\]
Therefore, the two points are: - C (0, 4) and D (1, 0).
So, the graph of the two linear equations can be plotted as: -

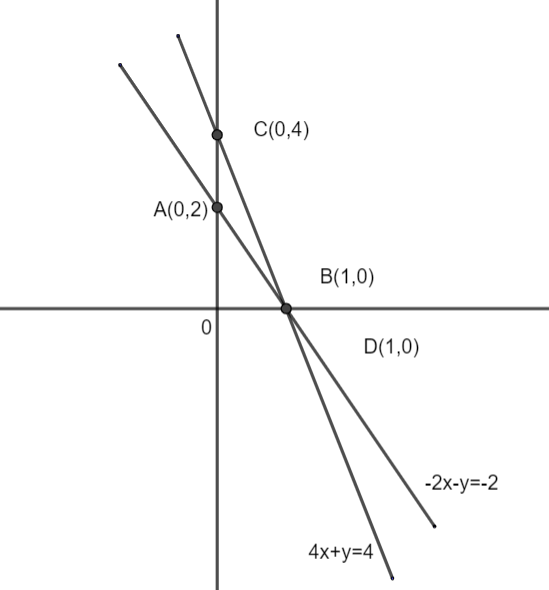
From the above graph we can clearly see that the two straight lines are interesting at point B or D both of whose coordinates are (1, 0). So, point B or D is the solution of the given system of equations.

Note: One may note that we can check our answer by solving the equations of the two given lines algebraically. If we will get the same coordinate of P as in the graph then our answer will be correct. Remember that while drawing the graph, substitute x = 0 and y = 0 to determine the points. If we will use any other values of x and y then we will have to do some calculations to draw the graph. Do not forget to draw and mark important points where the lines cut the axes.