Question

How do you solve the system 2x + 3y = 7 and 2x – 3y = 13 by graphing?

Answer 1

Hint: Draw the graph of the two given equations. To draw the graph of a straight line, we need at least two points. So, choose one of the equations and substitute x = 0, determine y, then substitute y = 0, determine x. Now, apply the same process for the second equation. Plot the graph of the two equations using the points obtained. Check the point of intersection to get the answer.

Complete step by step answer:
Let us assume the two equations as: -
\[\Rightarrow 2x+3y=7\] - (1)
\[\Rightarrow 2x-3y=13\] - (2)
Considering equation (1), we have,
\[\Rightarrow 2x+3y=7\]
Substituting x = 0, we get,
\[\begin{align}
  & \Rightarrow 3y=7 \\
 & \Rightarrow y=\dfrac{7}{3} \\
\end{align}\]
Substituting y = 0, we get,
\[\begin{align}
  & \Rightarrow 2x=7 \\
 & \Rightarrow x=\dfrac{7}{2} \\
\end{align}\]
Therefore, the two points are: - \[A\left( 0,\dfrac{7}{3} \right)\] and \[B\left( \dfrac{7}{2},0 \right)\].
Now, considering equation (2), we have,
\[\Rightarrow 2x-3y=13\]
Substituting x = 0, we get,
\[\begin{align}
  & \Rightarrow -3y=13 \\
 & \Rightarrow y=\dfrac{-13}{3} \\
\end{align}\]
Substituting y = 0, we get,
\[\begin{align}
  & \Rightarrow 2x=13 \\
 & \Rightarrow x=\dfrac{13}{2} \\
\end{align}\]
Therefore, the points are: - \[C\left( 0,\dfrac{-13}{3} \right)\] and \[D\left( \dfrac{13}{2},0 \right)\].
So, the graph of the two functions can be plotted as: -

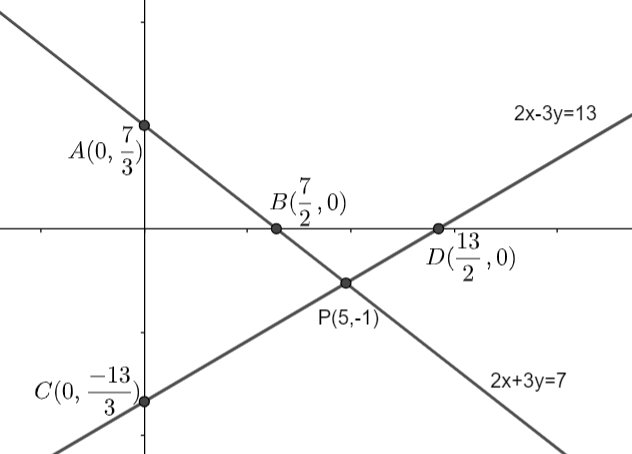
Here, we are assuming the point of intersection of the two lines as P. On observing the graph we can see that the point of intersection of the two lines is given by the coordinates P (5, -1).

Note:
One may note that we can check our answer by solving the equations of the two given lines algebraically. If we will get the same coordinate of P as in the graph then our answer will be correct. Remember that while drawing the graph, substitute x = 0 and y = 0 to determine the points. If we will use any other values of x and y then we will have to do some calculations to draw the graph. Do not forget to draw and mark important points on the graph like the points where the lines cut the axes.