Question

How do you solve the system $2x+3y=18$ and $4x-3y=0$ ?

Answer 1

Hint: We solve this problem graphically. We express the given lines in the intercept form $\dfrac{x}{a}+\dfrac{y}{b}=1$ and then draw the respective lines. The point where these two lines intersect is the answer to the given set of equations.

Complete step-by-step solution:
The given equations that we have are
$2x+3y=18....\left( 1 \right)$
$4x-3y=0....\left( 2 \right)$
We solve the two equations by graphical method. For this, we need to rewrite the equations in some standard form to draw their graphs easily. For this problem, the standard form that we use will be the intercept form. The intercept form of a straight line is
$\dfrac{x}{a}+\dfrac{y}{b}=1$
Where, $a$ in the $x$ -intercept and $b$ is the $y$ -intercept.
We start by rearranging the equation $\left( 1 \right)$ in the intercept form. For this, we divide both sides of the equation by $18$ . The equation thus becomes,
$\Rightarrow \dfrac{2x}{18}+\dfrac{3y}{18}=1$
The above equation can be written as,
$\Rightarrow \dfrac{x}{\dfrac{18}{2}}+\dfrac{y}{\dfrac{18}{3}}=1$
Simplifying the above equation, we get,
$\Rightarrow \dfrac{x}{9}+\dfrac{y}{6}=1$
After comparing the above equation with the general intercept form, we get $a=9,b=6$ . Keeping these intercepts in mind, we draw the line on the graph.
Similarly, we rewrite the equation $\left( 2 \right)$ in the intercept form. But, if we carefully observe, we can see that it cannot be expressed in the intercept form as the value of the intercepts are $0$ . This line thus passes through the origin. Also, we can see that the point $\left( 3,4 \right)$ lies on the point apart from the origin. Thus, we join the points $\left( 0,0 \right)$ and $\left( 3,4 \right)$ to get the line.

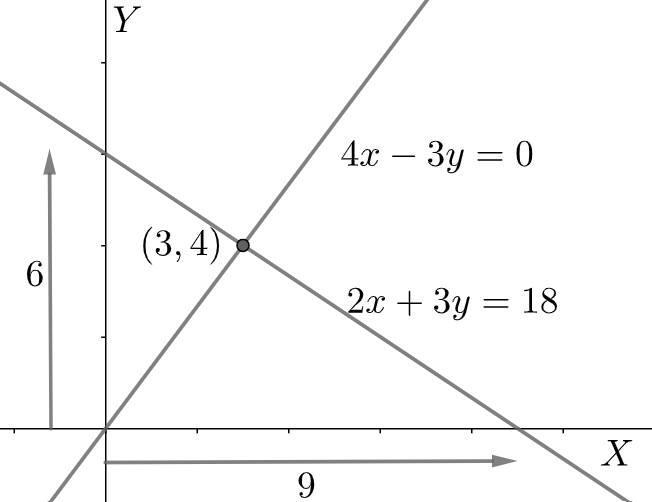
We see that the two lines intersect at the point $\left( 3,4 \right)$ .
Therefore, we can conclude that the solution of the given set of equations is $x=3,y=4$.

Note: In this problem, we must be careful to observe that the second line has no intercepts. Students often mistake by taking the intercepts to be $3$ and $4$ , and draw a wrong line. This gives wrong results. This problem can also be solved by the substitution method, where we substitute one equation into the other to get the solution.