Question

How do you solve the right triangle ABC given $B={{45}^{\circ }}$ , $C={{90}^{\circ }}$ and side $AB=5$ units?

Answer 1

Hint: In this problem, as we are given the two angles out of the three, then we should at first find out the third angle using the property $A+B+C={{180}^{\circ }}$ . After that, since ABC is right triangle, we should find the remaining two sides by taking the projection of side AB at angles $B={{45}^{\circ }}$ , $C={{90}^{\circ }}$ .

Complete step by step answer:
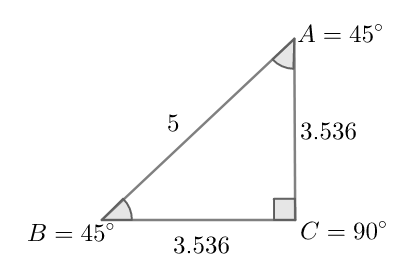
In this problem, we are given a right triangle with $B={{45}^{\circ }}$ , $C={{90}^{\circ }}$ and side $AB=5$ units. By solving for the right triangle, we mean to find all the remaining sides and angles of the right triangle ABC. This can be done by using various properties of a triangle, especially a right triangle.
At first, we see that the values of two angles of the right triangle ABC are given. This implies that the third angle can be found out easily using the property of a triangle that the sum of internal angles of a triangle is ${{180}^{\circ }}$ . In other words,
$\begin{align}
  & \Rightarrow A+B+C={{180}^{\circ }} \\
 & \Rightarrow A+{{45}^{\circ }}+{{90}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow A={{45}^{\circ }} \\
\end{align}$
We can now draw the right triangle ABC. Clearly, side AB is the hypotenuse. The sides AC and BC are the projections on of the side AB at an angle ${{45}^{\circ }}$ . This means that we can use the trigonometric relations over here.
$\begin{align}
  & AC=AB\sin {{45}^{\circ }} \\
 & \Rightarrow AC=5\times \dfrac{1}{\sqrt{2}} \\
 & \Rightarrow AC=3.536\text{ }units \\
\end{align}$
Similarly,
$\begin{align}
  & BC=AB\cos {{45}^{\circ }} \\
 & \Rightarrow BC=5\times \dfrac{1}{\sqrt{2}} \\
 & \Rightarrow BC=3.536\text{ }units \\
\end{align}$
Therefore, we can conclude that the three sides of the triangle are $AC=3.536\text{ }units,BC=3.536\text{ }units,AB=5\text{ }units$ and angles are $A={{45}^{\circ }},B={{45}^{\circ }},C={{90}^{\circ }}$ .

Note: In this problem, as the triangle is right angled as well as isosceles, the calculations have become a lot easier. But, if the triangle were not isosceles, then we must be careful with the calculations. This problem can also be solved by using the Lami’s theorem which is,
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$ where, a, b and c are the three sides of the triangle ABC opposite to the angles A, B and C.