
How do you solve the quadratic $3{{x}^{2}}-2x=2x+7$ using any method?
Answer
545.4k+ views
Hint: For this problem we need to solve the given quadratic equation. We know that the general form of the quadratic equation is $a{{x}^{2}}+bx+c=0$. So, we will convert the given equation in the general form of quadratic equation by applying some arithmetic operations. Now we will compare the obtained equation with the general form of the quadratic equation and write the values of $a$, $b$, $c$. After that we will use the quadratic formula which is $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$ and substitute the values of $a$, $b$, $c$ to get the required solution of the given equation.
Complete step by step solution:
The quadratic equation is $3{{x}^{2}}-2x=2x+7$.
Subtracting $2x+7$ on both sides of the above equation, then we will get
$\begin{align}
& \Rightarrow 3{{x}^{2}}-2x-\left( 2x+7 \right)=\left( 2x+7 \right)-\left( 2x+7 \right) \\
& \Rightarrow 3{{x}^{2}}-4x-7=0 \\
\end{align}$
Comparing the above equation with general form of the quadratic equation which is $a{{x}^{2}}+bx+c=0$, then we will get
$a=3$, $b=-4$, $c=-7$.
We know that the solution of the equation $a{{x}^{2}}+bx+c=0$ is $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$. From this the solution of the given equation will be calculated by substituting $a=3$, $b=-4$, $c=-7$ in the above formula, then we will get
$\begin{align}
& \Rightarrow x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} \\
& \Rightarrow x=\dfrac{-\left( -4 \right)\pm \sqrt{{{\left( -4 \right)}^{2}}-4\left( 3 \right)\left( -7 \right)}}{2\left( 3 \right)} \\
\end{align}$
When we multiply a negative sign with negative sign, we will get positive sign as result, then the above equation is modified as
$\begin{align}
& \Rightarrow x=\dfrac{4\pm \sqrt{16+84}}{6} \\
& \Rightarrow x=\dfrac{4\pm \sqrt{100}}{6} \\
\end{align}$
Considering the value $\sqrt{100}$. We can write the value $\sqrt{100}=\sqrt{{{10}^{2}}}=10$ in the above equation, then we will get
$\begin{align}
& \Rightarrow x=\dfrac{4\pm 10}{6} \\
& \Rightarrow x=\dfrac{4+10}{6}\text{ or }\dfrac{4-10}{6} \\
& \Rightarrow x=\dfrac{14}{6}\text{ or }-\dfrac{6}{6} \\
& \Rightarrow x=\dfrac{7}{3}\text{ or }-1 \\
\end{align}$
Hence the solution of the given equation $3{{x}^{2}}-2x=2x+7$ is $x=\dfrac{7}{3},-1$.
Note: We can also use different methods from factorization method, completing squares method, graphical method. Another simplest method is a graphical method. In this method we will plot the graph of the given equation and note the points where the given line meets the $x-axis$ as a solution of the equation. We can observe the graph of the given equation as
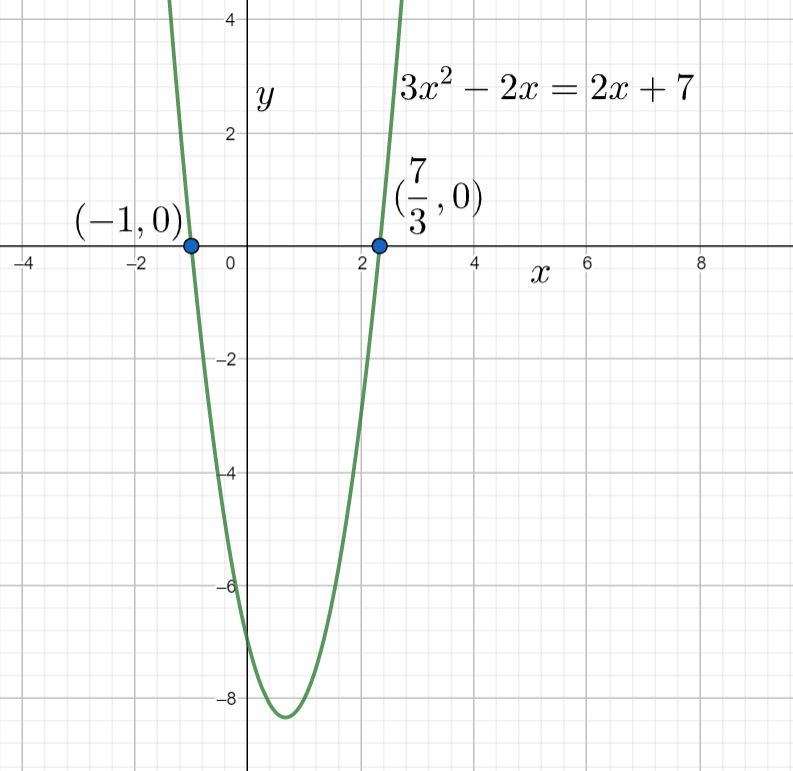
Complete step by step solution:
The quadratic equation is $3{{x}^{2}}-2x=2x+7$.
Subtracting $2x+7$ on both sides of the above equation, then we will get
$\begin{align}
& \Rightarrow 3{{x}^{2}}-2x-\left( 2x+7 \right)=\left( 2x+7 \right)-\left( 2x+7 \right) \\
& \Rightarrow 3{{x}^{2}}-4x-7=0 \\
\end{align}$
Comparing the above equation with general form of the quadratic equation which is $a{{x}^{2}}+bx+c=0$, then we will get
$a=3$, $b=-4$, $c=-7$.
We know that the solution of the equation $a{{x}^{2}}+bx+c=0$ is $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$. From this the solution of the given equation will be calculated by substituting $a=3$, $b=-4$, $c=-7$ in the above formula, then we will get
$\begin{align}
& \Rightarrow x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} \\
& \Rightarrow x=\dfrac{-\left( -4 \right)\pm \sqrt{{{\left( -4 \right)}^{2}}-4\left( 3 \right)\left( -7 \right)}}{2\left( 3 \right)} \\
\end{align}$
When we multiply a negative sign with negative sign, we will get positive sign as result, then the above equation is modified as
$\begin{align}
& \Rightarrow x=\dfrac{4\pm \sqrt{16+84}}{6} \\
& \Rightarrow x=\dfrac{4\pm \sqrt{100}}{6} \\
\end{align}$
Considering the value $\sqrt{100}$. We can write the value $\sqrt{100}=\sqrt{{{10}^{2}}}=10$ in the above equation, then we will get
$\begin{align}
& \Rightarrow x=\dfrac{4\pm 10}{6} \\
& \Rightarrow x=\dfrac{4+10}{6}\text{ or }\dfrac{4-10}{6} \\
& \Rightarrow x=\dfrac{14}{6}\text{ or }-\dfrac{6}{6} \\
& \Rightarrow x=\dfrac{7}{3}\text{ or }-1 \\
\end{align}$
Hence the solution of the given equation $3{{x}^{2}}-2x=2x+7$ is $x=\dfrac{7}{3},-1$.
Note: We can also use different methods from factorization method, completing squares method, graphical method. Another simplest method is a graphical method. In this method we will plot the graph of the given equation and note the points where the given line meets the $x-axis$ as a solution of the equation. We can observe the graph of the given equation as

Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

The draft of the Preamble of the Indian Constitution class 10 social science CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who gave "Inqilab Zindabad" slogan?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Who is the Brand Ambassador of Incredible India?




