Question

How do you solve the polynomial inequality and state the answer in interval notation given $ 3{x^2} + 2x < {x^4} $ ?

Answer 1

Hint: In the given question, we are required to find the answer in interval notation to the inequality given to us in the problem itself. So, we first transpose or shift all the terms to one side of the equation and look for methods of simplification and factorization. We may also employ the wavy curve method that represents the graph of the function and helps us to solve the inequality graphically.

Complete step by step solution:
So, we are given the inequality $ 3{x^2} + 2x < {x^4} $ .
Shifting all the terms to the right side of the equation, we get,
 $ \Rightarrow {x^4} - 3{x^2} - 2x > 0 $
 $ \Rightarrow x\left( {{x^3} - 3x - 2} \right) > 0 $
Now, to solve the inequality, we first need to factorize the cubic expression written in brackets.
So, we have $ \left( {{x^3} - 3x - 2} \right) $ .
Hence, by hit and trial, we notice that for $ x = 2 $ , the value of the expression is $ 0 $ .
So, we infer that $ \left( {x - 2} \right) $ is a factor of $ \left( {{x^3} - 3x - 2} \right) $ .
So, we can divide $ \left( {{x^3} - 3x - 2} \right) $ by $ \left( {x - 2} \right) $ so as to find the other factors or we can either simply factorize $ \left( {{x^3} - 3x - 2} \right) $ .
So, $ \left( {{x^3} - 3x - 2} \right) = \left( {x - 2} \right)\left( {{x^2} + 2x + 1} \right) $
Condensing the quadratic factor $ \left( {{x^2} + 2x + 1} \right) $ into squares of binomial $ \left( {x + 1} \right) $ .
 $ \Rightarrow \left( {{x^3} - 3x - 2} \right) = \left( {x - 2} \right){\left( {x + 1} \right)^2} $
Hence, getting back to the inequality, we get,
 $ \Rightarrow x\left( {x - 2} \right){\left( {x + 1} \right)^2} > 0 $
Now, using the graphical method so as to find the intervals in which the inequality holds.
Graph of polynomial function $ x\left( {x - 2} \right){\left( {x + 1} \right)^2} $ is as follows:

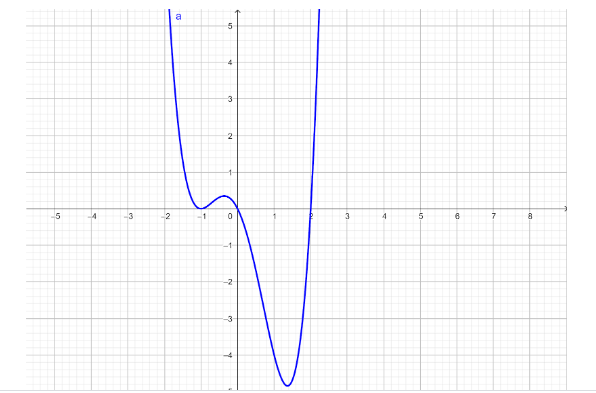
So, we can observe from the graph of polynomial function $ x\left( {x - 2} \right){\left( {x + 1} \right)^2} $ that the value of the function is positive for the intervals $ \left( { - \inf , - 1} \right) $ , $ \left( { - 1,0} \right) $ and $ \left( {2,\inf } \right) $ . We
So, the solution to the polynomial inequality $ 3{x^2} + 2x < {x^4} $ is the union of the intervals $ \left( { - \inf , - 1} \right) $ , $ \left( { - 1,0} \right) $ and $ \left( {2,\inf } \right) $ as the inequality $ 3{x^2} + 2x < {x^4} $ is same as $ {x^4} - 3{x^2} - 2x > 0 $ .

Note: So, these kinds of questions which require us to solve the two sided inequalities can be solved by following some basic algebraic rules such as transposition and factorization. Wavy curve methods may also be employed in some complex inequalities.