Question

Solve the pair of linear equations
$\dfrac{1}{3x+y}+\dfrac{1}{3x-y}=\dfrac{3}{4}$
$\dfrac{1}{2\left( 3x+y \right)}-\dfrac{1}{2\left( 3x-y \right)}=-\dfrac{1}{8}$
$3x+y\ne 0$ and $3x-y\ne 0$

Answer 1

Hint: Assume $a=\dfrac{1}{3x+y}$ and $b=\dfrac{1}{3x-y}$. Hence form two linear equations in a and b. Solve for a and b. Now revert to original variables and hence form two linear equations in x and y. Solve for x and y. Remove extraneous roots, i.e. those roots at which either a or b is not defined.

Complete step-by-step answer:
Let $a=\dfrac{1}{3x+y}$ and $b=\dfrac{1}{3x-y}$.
Since $\dfrac{1}{3x+y}+\dfrac{1}{3x-y}=\dfrac{3}{4}$, we have
$a+b=\dfrac{3}{4}\text{ (i)}$
Also since $\dfrac{1}{2\left( 3x+y \right)}-\dfrac{1}{2\left( 3x-y \right)}=-\dfrac{1}{8}$ , we have
$\dfrac{a}{2}+\dfrac{b}{2}=\dfrac{-1}{8}$
Multiplying both sides by 2, we get
$\begin{align}
  & \dfrac{2a}{2}-\dfrac{2b}{2}=\dfrac{-2}{8} \\
 & \Rightarrow a-b=\dfrac{-1}{4}\text{ (ii)} \\
\end{align}$
Adding equation (i) and equation (ii), we get
$\begin{align}
  & a+b+a-b=\dfrac{3}{4}-\dfrac{1}{4} \\
 & \Rightarrow 2a=\dfrac{1}{2} \\
\end{align}$
Dividing both sides by 2, we get
$a=\dfrac{1}{2\times 2}=\dfrac{1}{4}$
Substituting the value of “a” in equation (i), we get
$\begin{align}
  & a+b=\dfrac{3}{4} \\
 & \Rightarrow \dfrac{1}{4}+b=\dfrac{3}{4} \\
 & \Rightarrow b=\dfrac{3}{4}-\dfrac{1}{4}=\dfrac{2}{4}=\dfrac{1}{2} \\
\end{align}$
Hence, we have $a=\dfrac{1}{4}$ and $b=\dfrac{1}{2}$
Reverting to original variables, we get
$\begin{align}
  & \dfrac{1}{3x+y}=\dfrac{1}{4} \\
 & \\
\end{align}$
Taking reciprocals on both sides, we get
$3x+y=4\text{ (iii)}$
and
$\dfrac{1}{3x-y}=\dfrac{1}{2}$
Taking reciprocals on both sides, we get
$3x-y=2\text{ (iv)}$
Adding equation (iii) and equation (iv), we get
$\begin{align}
  & 3x+y+3x-y=2+4 \\
 & \Rightarrow 6x=6 \\
 & \Rightarrow x=1 \\
\end{align}$
Substituting the value of x in equation (iii), we get
$\begin{align}
  & 3x+y=4 \\
 & \Rightarrow 3+y=4 \\
 & \Rightarrow y=4-3=1 \\
\end{align}$
Hence we have x=1 and y=1.
At x=1 ,y =1, 3x+y = 4 and 3x-y =2
Since $3x+y\ne 0$ and $3x-y\ne 0$, we have
(x,y) = (1,1) is the solution of the given system of equations.
Note: Visualising graphically.

If we plot the curves $\dfrac{1}{3x+y}+\dfrac{1}{3x-y}=\dfrac{3}{4}$ and $\dfrac{1}{2\left( 3x+y \right)}-\dfrac{1}{2\left( 3x-y \right)}=-\dfrac{1}{8}$ on the same graph paper, then these curves will intersect at the point (1,1).

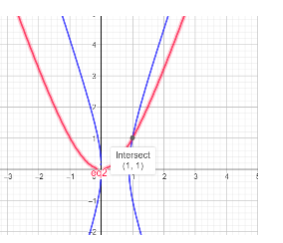
In the above graph, the blue curve is of $\dfrac{1}{3x+y}+\dfrac{1}{3x-y}=\dfrac{3}{4}$ equation and the pink curve of $\dfrac{1}{2\left( 3x+y \right)}-\dfrac{1}{2\left( 3x-y \right)}=-\dfrac{1}{8}$ equation. As can be seen from the graph, the two curves intersect at (1,1).