
Solve the modulus equation:
\[\left| \dfrac{{{x}^{2}}-8x+12}{{{x}^{2}}-10x+21} \right|=\dfrac{-\left( {{x}^{2}}-8x+12 \right)}{{{x}^{2}}-10x+21}\]
Answer
615.6k+ views
Hint: First of all, find the values at which the modulus function will change its sign by substituting \[{{x}^{2}}-8x+12=0\text{ and }{{x}^{2}}-10x+21=0\]. Now divide the number line into various intervals and check for each interval and solve the equation to get the solution. Also, remember that \[\left| x \right|=x\text{ for }x>0\] and \[\left| x \right|=-x\text{ for }x<0\].
Complete step-by-step answer:
In this question, we have to solve the modulus equation
\[\left| \dfrac{{{x}^{2}}-8x+12}{{{x}^{2}}-10x+21} \right|=\dfrac{-\left( {{x}^{2}}-8x+12 \right)}{{{x}^{2}}-10x+21}\]
Let us find the values at which the modulus function will change its signs.
\[{{x}^{2}}-8x+12=0\]
We can also write the above equation as,
\[{{x}^{2}}-6x-2x+12=0\]
\[\Rightarrow x\left( x-6 \right)-2\left( x-6 \right)=0\]
\[\left( x-6 \right)\left( x-2 \right)=0\]
So, from this we get x = 6 or x = 2
\[{{x}^{2}}-10x+21=0\]
We can also write the above equation as,
\[{{x}^{2}}-7x-3x+21=0\]
\[\Rightarrow x\left( x-7 \right)-3\left( x-7 \right)=0\]
\[\left( x-3 \right)\left( x-7 \right)=0\]
So, from this we get, x = 3 and x = 7.
Now, let us consider the function given in the question
\[\left| \dfrac{{{x}^{2}}-8x+12}{{{x}^{2}}-10x+21} \right|=\dfrac{-\left( {{x}^{2}}-8x+12 \right)}{{{x}^{2}}-10x+21}\]
We can also write the above equation as,
\[\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}....\left( i \right)\]
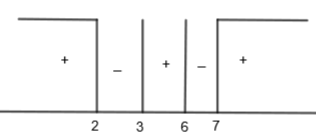
Now, we will check the values of the function at different intervals. Also \[x\ne 3,7\] because that will make the denominator 0 which is not possible. We also know that \[\left| x \right|=x\] where x > 0 and \[\left| x \right|=-x\] where x < 0. Let us take x > 7.
For x > 7, (x – 6) > 0, (x – 2) > 0, (x – 7) > 0, (x – 3) > 0
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}>0\]
\[\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
By using this in equation (i), we get,
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
Also, \[x\ne 7\text{ and }x\ne 3\]. So, by canceling the denominators, we get,
\[\left( x-6 \right)\left( x-2 \right)=-\left( x-6 \right)\left( x-2 \right)\]
\[\left( x-6 \right)\left( x-2 \right)+\left( x-6 \right)\left( x-2 \right)=0\]
\[2\left( x-6 \right)\left( x-2 \right)=0\]
\[\left( x-6 \right)\left( x-2 \right)=0\]
From this, we get, x = 6 or x = 2. But we have to take an interval x > 7. So, x could not be equal to 2 or 6. Similarly, let us take \[6\le x<7\].
For, \[6\le x<7,\left( x-6 \right)>0,\left( x-2 \right)>0,\left( x-7 \right)<0,\left( x-3 \right)>0\]
So, \[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}<0\]
\[\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
By using this in equation (i), we get,
\[\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
As \[x\ne 7\text{ and }x\ne 3\]. So, by canceling the denominator, we get,
\[-\left( x-6 \right)\left( x-2 \right)+\left( x+6 \right)\left( x-2 \right)=0\]
0 = 0
LHS = RHS
Since we have got LHS = RHS, that means all the values of this interval will satisfy the equation. So, we get, \[x\in [6,7)....\left( i \right)\]
Let us take 3 < x < 6.
For, 3 < x < 6, (x – 6) < 0, (x – 2) > 0, (x – 7) < 0, (x – 3) > 0
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}>0\]
\[\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
By using this in equation (i), we get,
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
As \[x\ne 7\text{ and }x\ne 3\]. So, by canceling the denominator, we get,
\[\left( x-6 \right)\left( x-2 \right)=-\left( x-6 \right)\left( x-2 \right)\]
\[\left( x-6 \right)\left( x-2 \right)+\left( x-6 \right)\left( x-2 \right)=0\]
\[2\left( x-6 \right)\left( x-2 \right)=0\]
\[\left( x-6 \right)\left( x-2 \right)=0\]
From this, we get, x = 6 or x = 2. But we have to take interval 3 < x < 6, so x could not be equal to 2 or 6.
Let us take \[2\le x<3\]
For, \[2\le x<3,\left( x-6 \right)<0,\left( x-2 \right)>0,\left( x-7 \right)<0,\left( x-3 \right)<0\]
So,
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}<0\]
So,
\[\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
By using this in equation (i), we get,
\[\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
As \[x\ne 7\text{ and }x\ne 3\]. So, by canceling the denominator, we get,
\[-\left( x-6 \right)\left( x-2 \right)+\left( x+6 \right)\left( x-2 \right)=0\]
\[0=0\]
LHS = RHS
Since we have got LHS = RHS, that means all the values of this interval will satisfy the equation.
So, we get, \[x\in [2,3)....\left( ii \right)\]
Now, let us take x < 2
For, x < 2, (x – 6) < 0, (x – 2) < 0, (x – 7) < 0, (x – 3) < 0
So,
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}>0\]
So,
\[\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
By using this in equation (i), we get,
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
As \[x\ne 7\text{ and }x\ne 3\]. So, by canceling the denominator, we get,
\[\left( x-6 \right)\left( x-2 \right)=-\left( x-6 \right)\left( x-2 \right)\]
\[\left( x-6 \right)\left( x-2 \right)+\left( x-6 \right)\left( x-2 \right)=0\]
\[2\left( x-6 \right)\left( x-2 \right)=0\]
\[\left( x-6 \right)\left( x-2 \right)=0\]
From this we get x = 6 or x = 2. But we have to take the interval x < 2, so x could not be equal to 2 or 6.
So, from (i) and (ii), we get,
\[x\in [2,3)\cup [6,7)\]
Note: Here, students can cross-check their answer by substituting any value of x from \[[2,3)\cup [6,7)\] and checking if LHS = RHS. Also, students must note that whenever we get LHS = RHS after solving the equation, then that equation is true for all the values of x in the domain of the equation that we have taken. Also, we can only cancel factors from LHS and RHS of the equation, if they are not equal to zero otherwise we may miss some roots.
Complete step-by-step answer:
In this question, we have to solve the modulus equation
\[\left| \dfrac{{{x}^{2}}-8x+12}{{{x}^{2}}-10x+21} \right|=\dfrac{-\left( {{x}^{2}}-8x+12 \right)}{{{x}^{2}}-10x+21}\]
Let us find the values at which the modulus function will change its signs.
\[{{x}^{2}}-8x+12=0\]
We can also write the above equation as,
\[{{x}^{2}}-6x-2x+12=0\]
\[\Rightarrow x\left( x-6 \right)-2\left( x-6 \right)=0\]
\[\left( x-6 \right)\left( x-2 \right)=0\]
So, from this we get x = 6 or x = 2
\[{{x}^{2}}-10x+21=0\]
We can also write the above equation as,
\[{{x}^{2}}-7x-3x+21=0\]
\[\Rightarrow x\left( x-7 \right)-3\left( x-7 \right)=0\]
\[\left( x-3 \right)\left( x-7 \right)=0\]
So, from this we get, x = 3 and x = 7.
Now, let us consider the function given in the question
\[\left| \dfrac{{{x}^{2}}-8x+12}{{{x}^{2}}-10x+21} \right|=\dfrac{-\left( {{x}^{2}}-8x+12 \right)}{{{x}^{2}}-10x+21}\]
We can also write the above equation as,
\[\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}....\left( i \right)\]

Now, we will check the values of the function at different intervals. Also \[x\ne 3,7\] because that will make the denominator 0 which is not possible. We also know that \[\left| x \right|=x\] where x > 0 and \[\left| x \right|=-x\] where x < 0. Let us take x > 7.
For x > 7, (x – 6) > 0, (x – 2) > 0, (x – 7) > 0, (x – 3) > 0
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}>0\]
\[\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
By using this in equation (i), we get,
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
Also, \[x\ne 7\text{ and }x\ne 3\]. So, by canceling the denominators, we get,
\[\left( x-6 \right)\left( x-2 \right)=-\left( x-6 \right)\left( x-2 \right)\]
\[\left( x-6 \right)\left( x-2 \right)+\left( x-6 \right)\left( x-2 \right)=0\]
\[2\left( x-6 \right)\left( x-2 \right)=0\]
\[\left( x-6 \right)\left( x-2 \right)=0\]
From this, we get, x = 6 or x = 2. But we have to take an interval x > 7. So, x could not be equal to 2 or 6. Similarly, let us take \[6\le x<7\].
For, \[6\le x<7,\left( x-6 \right)>0,\left( x-2 \right)>0,\left( x-7 \right)<0,\left( x-3 \right)>0\]
So, \[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}<0\]
\[\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
By using this in equation (i), we get,
\[\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
As \[x\ne 7\text{ and }x\ne 3\]. So, by canceling the denominator, we get,
\[-\left( x-6 \right)\left( x-2 \right)+\left( x+6 \right)\left( x-2 \right)=0\]
0 = 0
LHS = RHS
Since we have got LHS = RHS, that means all the values of this interval will satisfy the equation. So, we get, \[x\in [6,7)....\left( i \right)\]
Let us take 3 < x < 6.
For, 3 < x < 6, (x – 6) < 0, (x – 2) > 0, (x – 7) < 0, (x – 3) > 0
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}>0\]
\[\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
By using this in equation (i), we get,
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
As \[x\ne 7\text{ and }x\ne 3\]. So, by canceling the denominator, we get,
\[\left( x-6 \right)\left( x-2 \right)=-\left( x-6 \right)\left( x-2 \right)\]
\[\left( x-6 \right)\left( x-2 \right)+\left( x-6 \right)\left( x-2 \right)=0\]
\[2\left( x-6 \right)\left( x-2 \right)=0\]
\[\left( x-6 \right)\left( x-2 \right)=0\]
From this, we get, x = 6 or x = 2. But we have to take interval 3 < x < 6, so x could not be equal to 2 or 6.
Let us take \[2\le x<3\]
For, \[2\le x<3,\left( x-6 \right)<0,\left( x-2 \right)>0,\left( x-7 \right)<0,\left( x-3 \right)<0\]
So,
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}<0\]
So,
\[\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
By using this in equation (i), we get,
\[\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{-\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
As \[x\ne 7\text{ and }x\ne 3\]. So, by canceling the denominator, we get,
\[-\left( x-6 \right)\left( x-2 \right)+\left( x+6 \right)\left( x-2 \right)=0\]
\[0=0\]
LHS = RHS
Since we have got LHS = RHS, that means all the values of this interval will satisfy the equation.
So, we get, \[x\in [2,3)....\left( ii \right)\]
Now, let us take x < 2
For, x < 2, (x – 6) < 0, (x – 2) < 0, (x – 7) < 0, (x – 3) < 0
So,
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}>0\]
So,
\[\left| \dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)} \right|=\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
By using this in equation (i), we get,
\[\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}=\dfrac{\left( x-6 \right)\left( x-2 \right)}{\left( x-7 \right)\left( x-3 \right)}\]
As \[x\ne 7\text{ and }x\ne 3\]. So, by canceling the denominator, we get,
\[\left( x-6 \right)\left( x-2 \right)=-\left( x-6 \right)\left( x-2 \right)\]
\[\left( x-6 \right)\left( x-2 \right)+\left( x-6 \right)\left( x-2 \right)=0\]
\[2\left( x-6 \right)\left( x-2 \right)=0\]
\[\left( x-6 \right)\left( x-2 \right)=0\]
From this we get x = 6 or x = 2. But we have to take the interval x < 2, so x could not be equal to 2 or 6.
So, from (i) and (ii), we get,
\[x\in [2,3)\cup [6,7)\]
Note: Here, students can cross-check their answer by substituting any value of x from \[[2,3)\cup [6,7)\] and checking if LHS = RHS. Also, students must note that whenever we get LHS = RHS after solving the equation, then that equation is true for all the values of x in the domain of the equation that we have taken. Also, we can only cancel factors from LHS and RHS of the equation, if they are not equal to zero otherwise we may miss some roots.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

State and prove Bernoullis theorem class 11 physics CBSE

What steps did the French revolutionaries take to create class 11 social science CBSE

The transition element that has lowest enthalpy of class 11 chemistry CBSE

Can anyone list 10 advantages and disadvantages of friction




