Question

How do you solve the logarithmic expression $\ln x = 7.25$?

Answer 1

Hint: We have to find all possible values of $x$ satisfying a given equation. For this, first rewrite both sides in terms of the base $e$. To solve for $x$, rewrite the equation using properties of logarithms and solve for $x$. Since, exponentiation and log are inverse functions. So, use the exponential property of logarithm (ii). Then, convert the decimal exponent to a fractional exponent. Next, convert the decimal number to a fraction by placing the decimal number over a power of ten. Next, add the whole number to the left of the decimal. Next, reduce the fractional part of the mixed number. Then, convert the mixed number into an improper fraction and get the desired result.
Formula used:
Properties of Logarithm function: Following are some useful properties of logarithm function:
(i). ${\log _a}\left( {xy} \right) = {\log _a}\left| x \right| + {\log _a}\left| y \right|$, where $a > 0,a \ne 1$ and $xy > 0$
(ii). ${e^{\ln \left( x \right)}} = x$.

Complete step-by-step solution:
Given equation: $\ln x = 7.25$
We have to find all possible values of $x$ satisfying a given equation.
Rewrite both sides in terms of the base $e$.
To solve for $x$, rewrite the equation using properties of logarithms.
${e^{\ln \left( x \right)}} = {e^{7.25}}$
Solve for $x$.
Exponentiation and log are inverse functions.
Use the exponential property of logarithm, ${e^{\ln \left( x \right)}} = x$.
$ \Rightarrow x = {e^{7.25}}$
Convert the decimal exponent to a fractional exponent.
Convert the decimal number to a fraction by placing the decimal number over a power of ten. Since there are 2 numbers to the right of the decimal point, place the decimal number over ${10^2}$ (100). Next, add the whole number to the left of the decimal.
$ \Rightarrow x = {e^{7\dfrac{{25}}{{100}}}}$
Reduce the fractional part of the mixed number.
$ \Rightarrow x = {e^{7\dfrac{1}{4}}}$
Convert the mixed number $7\dfrac{1}{4}$ into an improper fraction first by multiplying the denominator (4) by the whole number part (7) and add the numerator (1) to get the new numerator. Place the new numerator (29) over the old denominator (4).
$\therefore x = {e^{\dfrac{{29}}{4}}}$
The result can be shown in multiple forms.
Exact Form: $x = {e^{\dfrac{{29}}{4}}}$
Decimal Form: $x = 1408.104848$
Therefore, $x = {e^{\dfrac{{29}}{4}}}$ or $x = 1408.104848$ is the only solution of $\ln x = 7.25$.

Note: In above question, we can find the solutions of given equation by plotting the equation, $\ln x = 7.25$ on graph paper and determine all its solutions.

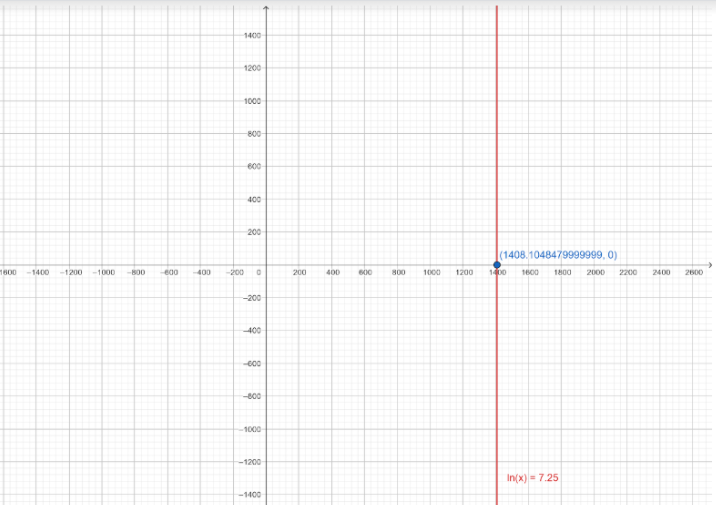
From the graph paper, we can see that $x = 1408.104848$ is the only solution of $\ln x = 7.25$.
Final solution: Therefore, $x = {e^{\dfrac{{29}}{4}}}$ or $x = 1408.104848$ is the only solution of $\ln x = 7.25$.