Question

Solve the linear inequalities: -
(i) \[\left| \dfrac{2}{x-4} \right|>1,x\ne 4\]
(ii) \[\left| x-1 \right|\le 5,\left| x \right|\ge 2\]

Answer 1

Hint: For part (i) of the given inequalities apply the formula: - if \[\left| x \right|>a\] then x < -a or x > a. Form two cases, the first one having the relation x < -a and the second one having the relation x >a. Take all the terms to the L.H.S and simplify the expression to obtain them in the form \[\dfrac{x-q}{x-p}<0\] whose solution is minimum {p, q} < x < maximum {p, q}. Take the union of the solution set of x in both the cases and get the answer. For part (ii) of the given inequalities apply the formula: - if \[\left| x \right|\le a\] then \[-a\le x\le a\]. Take the intersection of the solution set obtained with the given condition \[\left| x \right|\ge 2\] and get the answer.

Complete step-by-step answer:
Here, we have been provided with two inequalities containing modulus sign and we have to find the solution set of x. So, let us check them one – by – one.
(i) \[\left| \dfrac{2}{x-4} \right|>1,x\ne 4\]
We know that if \[\left| x \right|>a\], then x < -a or x > a, so here on removing the modulus sign we get,
\[\Rightarrow \dfrac{2}{x-4}<-1\] or \[\dfrac{2}{x-4}>1\]
So, here two cases can be formed. Let us check them one – by – one.
(1). Case 1: - Considering \[\dfrac{2}{x-4}<-1\]
\[\begin{align}
  & \Rightarrow \dfrac{2}{x-4}+1<0 \\
 & \Rightarrow \dfrac{2+x-4}{x-4}<0 \\
 & \Rightarrow \dfrac{x-2}{x-4}<0 \\
\end{align}\]
Now, we know that the solution set of the inequality of the form \[\dfrac{x-q}{x-p}<0\] is given as: - minimum {p, q} < x < maximum {p, q}. So, we have,
\[\Rightarrow \] minimum {2, 4} < x < maximum {2, 4}
\[\Rightarrow \] 2 < x < 4 – (1)

(2) Case 2: - Considering \[\dfrac{2}{x-4}>1\]
\[\begin{align}
  & \Rightarrow \dfrac{2}{x-4}-1>0 \\
 & \Rightarrow \dfrac{2-x+4}{x-4}>0 \\
 & \Rightarrow \dfrac{6-x}{x-4}>0 \\
\end{align}\]
Multiplying both sides with (-1) and reversing the direction of inequality, we get,
\[\begin{align}
  & \Rightarrow \left( -1 \right)\times \dfrac{6-x}{x-4}<\left( -1 \right)\times 0 \\
 & \Rightarrow \dfrac{x-6}{x-4}<0 \\
\end{align}\]
\[\Rightarrow \] minimum {6, 4} < x < maximum {6, 4}
\[\Rightarrow \] 4 < x < 6 – (2)
Now, either of the two cases will satisfy the given inequality, so we have to take union of sets of values of x obtained. Therefore, we have,

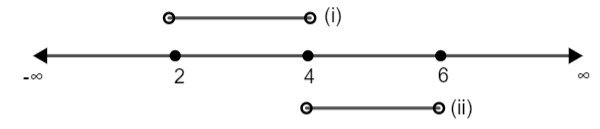
So, the solution set is given as: - \[x\in \left( 2,4 \right)\cup \left( 4,6 \right)\].
(ii) \[\left| x-1 \right|\le 5,\left| x \right|\ge 2\]
Here, we have to find the solution set of the inequality \[\left| x-1 \right|\le 5\] with the given condition \[\left| x \right|\ge 2\].
Now, we know that if \[\left| x \right|\le a\], then \[-a\le x\le a\], so here on removing the modulus sign we get,
\[\Rightarrow -5\le x-1\le 5\]
Adding 1 in all the terms, we get,
\[\Rightarrow -4\le x\le 6\] - (iii)
Now, the given condition is \[\left| x \right|\ge 2\], so applying the formula: - if \[\left| x \right|\ge a\] then \[x\le -a\] or \[x\ge a\], we get,
\[\Rightarrow x\le -2\] or \[x\ge 2\] - (iv)
Now, the situation set of x will be given as the intersection of sets of x obtained in equation (iii) and (iv) because we have to satisfy both the conditions. Therefore, we have,

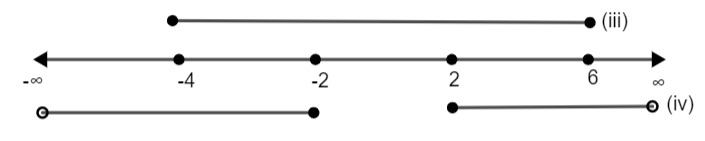
So, the solution set is given as: - \[x\in \left[ -4,-2 \right]\cup \left[ 2,6 \right]\].

Note: You must remember the properties and formulas of modulus to solve the above question. You may note that in the first inequality we have taken the union of the sets of values of x. This is because there we had to satisfy any of the two conditions. But in the second part we needed to satisfy both the conditions so we took the intersection of the sets.