Question

Solve the linear equations $11x+15y+23=0$ and $7x-2y-20=0$ by elimination method.

Answer 1

Hint: In the given question we are given two linear equations which we need to solve for two unknown variables x and y. Also, we need to use the elimination method in which we try to eliminate one variable and then compute the value of another variable.

Complete step-by-step solution:
According to the question we need to solve the two linear equations $11x+15y+23=0$and $7x-2y-20=0$ using elimination method which means we need to make the coefficients of any one variable same in both the equation and then subtract or add the equation so that the chosen variable gets removed and we get the value of another variable and repeat the same steps for another variable also.

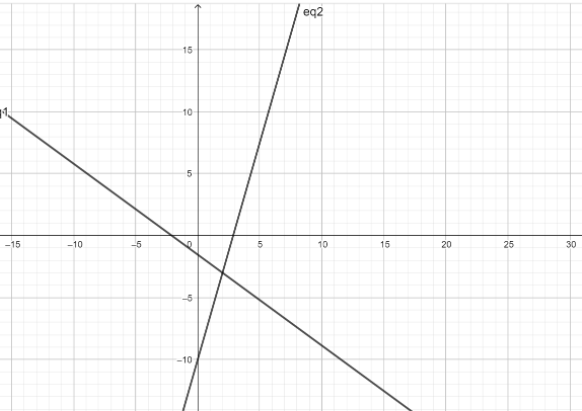
So, now let us multiply equation 1 by 7 and equation 2 by 11 and we get the following equations:
$77x+105y+161=0$
$77x-22y-220=0$
Now, subtracting these two equations we get
$\begin{align}
  & 127y+381=0 \\
 & \Rightarrow y=-\dfrac{381}{127} \\
 & \Rightarrow y=-3 \\
\end{align}$
Therefore, the required value of y is -3.
Similarly, now multiplying equation 1 by 2 and equation 2 by 15 we get the following equations:
$22x+30y+46=0$
$105x-30y-300=0$
Now, adding these two equations we get
$\begin{align}
  & 127x-254=0 \\
 & \Rightarrow 127x=254 \\
 & \Rightarrow x=\dfrac{254}{127} \\
 & \Rightarrow x=2 \\
\end{align}$
Therefore, the required value of x is 2.
Hence, the solution of two linear equations is \[x=2\] and \[y=-3\] .

Note: We need to be specific in the method to solve such linear equations and also be careful while eliminating the variable and make sure that the fractional coefficients are removed in order to simplify the given equations as the answer would be the same in that case also.