Solve the linear equation system using cross multiplication
1. 4x + 3y = 17
3x - 4y + 6 = 0
2. 5x + 4y + 14 = 0
3x = - 10 - 4y
3. 4x - 3y = 0
2x + 3y = 18
4. 4x + 6y = 15
3x - 4y = 7
Answer
Verified590.4k+ views
Hint: We will use the cross multiplication method here. This method is done on the equations of the form ax + by + c = 0 and dx + ey + f = 0. So on applying cross multiplication over these we will get a chart like so,
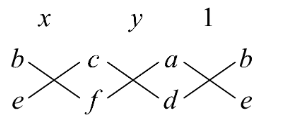
This will help in solving the equation for x and y.
Complete step-by-step solution -
Before proceeding to the solution we will first understand the concept of cross multiplication here. The method is done on the equations of the form ax + by + c = 0 and dx + ey + f = 0. So on applying cross multiplication over these we will get a chart as shown below
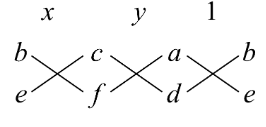
After evaluating it by expanding it with the help of crosses we will get $\dfrac{x}{bf-ec}=\dfrac{y}{cd-af}=\dfrac{1}{ae-bd}$. Now by equating the variable x with the constant 1 we will get $\dfrac{x}{bf-ec}=\dfrac{1}{ae-bd}...(i)$. And equating the variable y with the constant 1 we will get $\dfrac{y}{cd-af}=\dfrac{1}{ae-bd}...(ii)$.
1. Now, we will solve the equation one by one. We will consider the equation 4x + 3y = 17, 3x - 4y + 6 = 0.
As the equation 4x + 3y = 17 can be written as 4x + 3y – 17 = 0. So, according to the above method and step we will put all these coefficients a = 4, b = 3, c = - 17, d = 3, e = - 4 and f = 6 into equation (i). Thus we get
$\begin{align}
& \dfrac{x}{\left( 3 \right)\left( 6 \right)-\left( -4 \right)\left( -17 \right)}=\dfrac{1}{\left( 4 \right)\left( -4 \right)-\left( 3 \right)\left( 3 \right)} \\
& \Rightarrow \dfrac{x}{18-68}=\dfrac{1}{-16-9} \\
& \Rightarrow \dfrac{x}{-50}=-\dfrac{1}{25} \\
& \Rightarrow x=\dfrac{-50}{-25} \\
& \Rightarrow x=2 \\
\end{align}$
And after substituting the values in equation (ii) we will get
$\begin{align}
& \dfrac{y}{\left( -17 \right)\left( 3 \right)-\left( 4 \right)\left( +6 \right)}=\dfrac{1}{\left( 4 \right)\left( -4 \right)-\left( 3 \right)\left( 3 \right)} \\
& \Rightarrow \dfrac{y}{-51-24}=\dfrac{1}{-16-9} \\
& \Rightarrow \dfrac{y}{-75}=-\dfrac{1}{25} \\
& \Rightarrow y=\dfrac{-75}{-25} \\
& \Rightarrow y=3 \\
\end{align}$
Hence, the value of x = 2 and y = 3.
2. Now, we will solve the equation one by one. We will consider the equation 5x + 4y + 14 = 0, 3x = - 10 - 4y.
As the equation 3x = - 10 - 4y can be written as 3x + 4y + 10 = 0. So, according to the above method and step we will put all these coefficients a = 5, b = 4, c = 14, d = 3, e = 4 and f = 10 into equation (i). Thus we get
$\begin{align}
& \dfrac{x}{bf-ec}=\dfrac{1}{ae-bd} \\
& \dfrac{x}{\left( 4 \right)\left( 10 \right)-\left( 4 \right)\left( 14 \right)}=\dfrac{1}{\left( 5 \right)\left( 4 \right)-\left( 4 \right)\left( 3 \right)} \\
& \Rightarrow \dfrac{x}{40-56}=\dfrac{1}{20-12} \\
& \Rightarrow \dfrac{x}{-16}=-\dfrac{1}{8} \\
& \Rightarrow x=\dfrac{-16}{8} \\
& \Rightarrow x=-2 \\
\end{align}$
And after substituting the values in equation (ii) we will get
$\begin{align}
& \dfrac{y}{cd-af}=\dfrac{1}{ae-bd} \\
& \dfrac{y}{\left( 14 \right)\left( 3 \right)-\left( 5 \right)\left( 10 \right)}=\dfrac{1}{\left( 5 \right)\left( 4 \right)-\left( 4 \right)\left( 3 \right)} \\
& \Rightarrow \dfrac{y}{42-50}=\dfrac{1}{20-12} \\
& \Rightarrow \dfrac{y}{-8}=\dfrac{1}{8} \\
& \Rightarrow y=\dfrac{-8}{8} \\
& \Rightarrow y=-1 \\
\end{align}$
Hence, the value of x = - 2 and y = - 1.
3. Now, we will solve the equation one by one. We will consider the equations 4x - 3y = 0, 2x + 3y = 18.
As the equation 2x + 3y = 18 can be written as 2x + 3y – 18 = 0. So, according to the above method and step we will put all these coefficients a = 4, b = - 3, c = 0, d = 2, e = 3 and f = – 18 into equation (i). Thus we get
$\begin{align}
& \dfrac{x}{bf-ec}=\dfrac{1}{ae-bd} \\
& \dfrac{x}{\left( -3 \right)\left( -18 \right)-\left( 3 \right)\left( 0 \right)}=\dfrac{1}{\left( 4 \right)\left( 3 \right)-\left( -3 \right)\left( 2 \right)} \\
& \Rightarrow \dfrac{x}{54-0}=\dfrac{1}{12+6} \\
& \Rightarrow \dfrac{x}{54}=\dfrac{1}{18} \\
& \Rightarrow x=\dfrac{54}{18} \\
& \Rightarrow x=3 \\
\end{align}$
And after substituting the values in equation (ii) we will get
$\begin{align}
& \dfrac{y}{cd-af}=\dfrac{1}{ae-bd} \\
& \dfrac{y}{\left( 0 \right)\left( 2 \right)-\left( 4 \right)\left( -18 \right)}=\dfrac{1}{\left( 4 \right)\left( 3 \right)-\left( -3 \right)\left( 2 \right)} \\
& \Rightarrow \dfrac{y}{0+72}=\dfrac{1}{12+6} \\
& \Rightarrow \dfrac{y}{72}=\dfrac{1}{18} \\
& \Rightarrow y=\dfrac{72}{18} \\
& \Rightarrow y=4 \\
\end{align}$
Hence, the value of x = 3 and y = 4.
4. Now, we will solve the equation one by one. We will consider the equations 4x + 6y = 15 and 3x - 4y = 7.
As the equation 4x + 6y = 15 can be written as 4x + 6y – 15 = 0. Also, as the equation 3x - 4y = 7 can be written as 3x - 4y – 7 = 0. So, according to the above method and step we will put all these coefficients a = 4, b = 6, c = - 15, d = 3, e = - 4 and f = – 7 into equation (i). Thus we get
$\begin{align}
& \dfrac{x}{bf-ec}=\dfrac{1}{ae-bd} \\
& \dfrac{x}{\left( 6 \right)\left( -7 \right)-\left( -4 \right)\left( -15 \right)}=\dfrac{1}{\left( 4 \right)\left( -4 \right)-\left( 6 \right)\left( 3 \right)} \\
& \Rightarrow \dfrac{x}{-42-60}=\dfrac{1}{-16-18} \\
& \Rightarrow \dfrac{x}{-102}=\dfrac{1}{-34} \\
& \Rightarrow x=\dfrac{-102}{-34} \\
& \Rightarrow x=3 \\
\end{align}$
And after substituting the values in equation (ii) we will get
$\begin{align}
& \dfrac{y}{cd-af}=\dfrac{1}{ae-bd} \\
& \dfrac{y}{\left( -15 \right)\left( 3 \right)-\left( 4 \right)\left( -7 \right)}=\dfrac{1}{\left( 4 \right)\left( -4 \right)-\left( 6 \right)\left( 3 \right)} \\
& \Rightarrow \dfrac{y}{-45+28}=\dfrac{1}{-16-18} \\
& \Rightarrow \dfrac{y}{-17}=\dfrac{1}{-34} \\
& \Rightarrow y=\dfrac{-17}{-34} \\
& \Rightarrow y=\dfrac{1}{2} \\
\end{align}$
Hence, the value of x = 3 and y = $\dfrac{1}{2}$.
Note: We can also solve this equation by elimination method, substitution method, and Cramer’s rule. But since it was specifically written in the question that it should only be done by cross multiplication that is why we have solved it. One should be aware of solving it in a different method. It can be possible that the answer will get right but there will be no marks for the method resulting in a wrong answer. While doing multiplication and substituting the values into the formulas one should focus on this which is placing the value. This is because there are so many values that are to be substituted here that mistakes can happen.
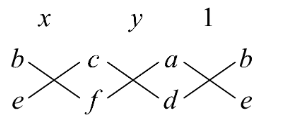
This will help in solving the equation for x and y.
Complete step-by-step solution -
Before proceeding to the solution we will first understand the concept of cross multiplication here. The method is done on the equations of the form ax + by + c = 0 and dx + ey + f = 0. So on applying cross multiplication over these we will get a chart as shown below
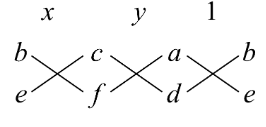
After evaluating it by expanding it with the help of crosses we will get $\dfrac{x}{bf-ec}=\dfrac{y}{cd-af}=\dfrac{1}{ae-bd}$. Now by equating the variable x with the constant 1 we will get $\dfrac{x}{bf-ec}=\dfrac{1}{ae-bd}...(i)$. And equating the variable y with the constant 1 we will get $\dfrac{y}{cd-af}=\dfrac{1}{ae-bd}...(ii)$.
1. Now, we will solve the equation one by one. We will consider the equation 4x + 3y = 17, 3x - 4y + 6 = 0.
As the equation 4x + 3y = 17 can be written as 4x + 3y – 17 = 0. So, according to the above method and step we will put all these coefficients a = 4, b = 3, c = - 17, d = 3, e = - 4 and f = 6 into equation (i). Thus we get
$\begin{align}
& \dfrac{x}{\left( 3 \right)\left( 6 \right)-\left( -4 \right)\left( -17 \right)}=\dfrac{1}{\left( 4 \right)\left( -4 \right)-\left( 3 \right)\left( 3 \right)} \\
& \Rightarrow \dfrac{x}{18-68}=\dfrac{1}{-16-9} \\
& \Rightarrow \dfrac{x}{-50}=-\dfrac{1}{25} \\
& \Rightarrow x=\dfrac{-50}{-25} \\
& \Rightarrow x=2 \\
\end{align}$
And after substituting the values in equation (ii) we will get
$\begin{align}
& \dfrac{y}{\left( -17 \right)\left( 3 \right)-\left( 4 \right)\left( +6 \right)}=\dfrac{1}{\left( 4 \right)\left( -4 \right)-\left( 3 \right)\left( 3 \right)} \\
& \Rightarrow \dfrac{y}{-51-24}=\dfrac{1}{-16-9} \\
& \Rightarrow \dfrac{y}{-75}=-\dfrac{1}{25} \\
& \Rightarrow y=\dfrac{-75}{-25} \\
& \Rightarrow y=3 \\
\end{align}$
Hence, the value of x = 2 and y = 3.
2. Now, we will solve the equation one by one. We will consider the equation 5x + 4y + 14 = 0, 3x = - 10 - 4y.
As the equation 3x = - 10 - 4y can be written as 3x + 4y + 10 = 0. So, according to the above method and step we will put all these coefficients a = 5, b = 4, c = 14, d = 3, e = 4 and f = 10 into equation (i). Thus we get
$\begin{align}
& \dfrac{x}{bf-ec}=\dfrac{1}{ae-bd} \\
& \dfrac{x}{\left( 4 \right)\left( 10 \right)-\left( 4 \right)\left( 14 \right)}=\dfrac{1}{\left( 5 \right)\left( 4 \right)-\left( 4 \right)\left( 3 \right)} \\
& \Rightarrow \dfrac{x}{40-56}=\dfrac{1}{20-12} \\
& \Rightarrow \dfrac{x}{-16}=-\dfrac{1}{8} \\
& \Rightarrow x=\dfrac{-16}{8} \\
& \Rightarrow x=-2 \\
\end{align}$
And after substituting the values in equation (ii) we will get
$\begin{align}
& \dfrac{y}{cd-af}=\dfrac{1}{ae-bd} \\
& \dfrac{y}{\left( 14 \right)\left( 3 \right)-\left( 5 \right)\left( 10 \right)}=\dfrac{1}{\left( 5 \right)\left( 4 \right)-\left( 4 \right)\left( 3 \right)} \\
& \Rightarrow \dfrac{y}{42-50}=\dfrac{1}{20-12} \\
& \Rightarrow \dfrac{y}{-8}=\dfrac{1}{8} \\
& \Rightarrow y=\dfrac{-8}{8} \\
& \Rightarrow y=-1 \\
\end{align}$
Hence, the value of x = - 2 and y = - 1.
3. Now, we will solve the equation one by one. We will consider the equations 4x - 3y = 0, 2x + 3y = 18.
As the equation 2x + 3y = 18 can be written as 2x + 3y – 18 = 0. So, according to the above method and step we will put all these coefficients a = 4, b = - 3, c = 0, d = 2, e = 3 and f = – 18 into equation (i). Thus we get
$\begin{align}
& \dfrac{x}{bf-ec}=\dfrac{1}{ae-bd} \\
& \dfrac{x}{\left( -3 \right)\left( -18 \right)-\left( 3 \right)\left( 0 \right)}=\dfrac{1}{\left( 4 \right)\left( 3 \right)-\left( -3 \right)\left( 2 \right)} \\
& \Rightarrow \dfrac{x}{54-0}=\dfrac{1}{12+6} \\
& \Rightarrow \dfrac{x}{54}=\dfrac{1}{18} \\
& \Rightarrow x=\dfrac{54}{18} \\
& \Rightarrow x=3 \\
\end{align}$
And after substituting the values in equation (ii) we will get
$\begin{align}
& \dfrac{y}{cd-af}=\dfrac{1}{ae-bd} \\
& \dfrac{y}{\left( 0 \right)\left( 2 \right)-\left( 4 \right)\left( -18 \right)}=\dfrac{1}{\left( 4 \right)\left( 3 \right)-\left( -3 \right)\left( 2 \right)} \\
& \Rightarrow \dfrac{y}{0+72}=\dfrac{1}{12+6} \\
& \Rightarrow \dfrac{y}{72}=\dfrac{1}{18} \\
& \Rightarrow y=\dfrac{72}{18} \\
& \Rightarrow y=4 \\
\end{align}$
Hence, the value of x = 3 and y = 4.
4. Now, we will solve the equation one by one. We will consider the equations 4x + 6y = 15 and 3x - 4y = 7.
As the equation 4x + 6y = 15 can be written as 4x + 6y – 15 = 0. Also, as the equation 3x - 4y = 7 can be written as 3x - 4y – 7 = 0. So, according to the above method and step we will put all these coefficients a = 4, b = 6, c = - 15, d = 3, e = - 4 and f = – 7 into equation (i). Thus we get
$\begin{align}
& \dfrac{x}{bf-ec}=\dfrac{1}{ae-bd} \\
& \dfrac{x}{\left( 6 \right)\left( -7 \right)-\left( -4 \right)\left( -15 \right)}=\dfrac{1}{\left( 4 \right)\left( -4 \right)-\left( 6 \right)\left( 3 \right)} \\
& \Rightarrow \dfrac{x}{-42-60}=\dfrac{1}{-16-18} \\
& \Rightarrow \dfrac{x}{-102}=\dfrac{1}{-34} \\
& \Rightarrow x=\dfrac{-102}{-34} \\
& \Rightarrow x=3 \\
\end{align}$
And after substituting the values in equation (ii) we will get
$\begin{align}
& \dfrac{y}{cd-af}=\dfrac{1}{ae-bd} \\
& \dfrac{y}{\left( -15 \right)\left( 3 \right)-\left( 4 \right)\left( -7 \right)}=\dfrac{1}{\left( 4 \right)\left( -4 \right)-\left( 6 \right)\left( 3 \right)} \\
& \Rightarrow \dfrac{y}{-45+28}=\dfrac{1}{-16-18} \\
& \Rightarrow \dfrac{y}{-17}=\dfrac{1}{-34} \\
& \Rightarrow y=\dfrac{-17}{-34} \\
& \Rightarrow y=\dfrac{1}{2} \\
\end{align}$
Hence, the value of x = 3 and y = $\dfrac{1}{2}$.
Note: We can also solve this equation by elimination method, substitution method, and Cramer’s rule. But since it was specifically written in the question that it should only be done by cross multiplication that is why we have solved it. One should be aware of solving it in a different method. It can be possible that the answer will get right but there will be no marks for the method resulting in a wrong answer. While doing multiplication and substituting the values into the formulas one should focus on this which is placing the value. This is because there are so many values that are to be substituted here that mistakes can happen.
Recently Updated Pages
Trending doubts
Who was the first woman to receive Bharat Ratna?
Write a letter to the principal requesting him to grant class 10 english CBSE
Why is there a time difference of about 5 hours between class 10 social science CBSE
What is the median of the first 10 natural numbers class 10 maths CBSE
The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths
Discuss the main reasons for poverty in India