
Solve the inequation \[5\left( {x - 2} \right) > 4\left( {x + 3} \right) - 24\] and represent its solution on a number line. Given the replacement set is $ - 4, - 3, - 2, - 1,0,1,2,3,4$ .
Answer
483.3k+ views
Hint: Here we are asked to find the solution set by using the given equation. First, we will try to solve the equation for $x$ then will find the solution set by using the given replacement set. And we are also asked to represent the solution in the number line so we will draw a number line and mark those points in the solution set.
Complete step-by-step answer:
It is given that the inequation is \[5\left( {x - 2} \right) > 4\left( {x + 3} \right) - 24\] and we aim to find the solution set for this inequation and represent them on the number line.
Let us first solve the given inequation.
The given inequation is \[5\left( {x - 2} \right) > 4\left( {x + 3} \right) - 24\] . let us first simplify it.
$ \Rightarrow 5x - 10 > 4x + 12 - 24$
Now let us take the terms having the unknown variable $x$ on one side and others on the other side.
$ \Rightarrow 5x - 4x > 10 - 12$
On simplifying it further we get
$ \Rightarrow x > - 2$
Now we can see that the solution is $ - 2$ .
The given replacement set is $\left\{ { - 4, - 3, - 2, - 1,0,1,2,3,4} \right\}$ the solution we got is $x > - 2$ so the solution set will be $\left\{ { - 1,0,1,2,3,4} \right\}$ .
We are also asked to represent those points in the number so let us first draw the number line.
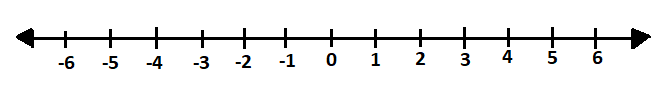
Now let us mark those points in the solution set.

Thus, we have found the solution set and also, we have represented them on the number line.
Note: While solving the inequation we are not supposed to make the inequality a symbol that may lead us to a wrong solution. In this problem, the given equation was an inequality while solving them we didn’t change the inequality sign. Also, we got the solution for x as $x > - 2$ since it is greater than minus two, we got the solution set from $ - 1$ to $4$ as per in the given replacement set. If the solution was greater than or equal to two then we have included the minus two.
Complete step-by-step answer:
It is given that the inequation is \[5\left( {x - 2} \right) > 4\left( {x + 3} \right) - 24\] and we aim to find the solution set for this inequation and represent them on the number line.
Let us first solve the given inequation.
The given inequation is \[5\left( {x - 2} \right) > 4\left( {x + 3} \right) - 24\] . let us first simplify it.
$ \Rightarrow 5x - 10 > 4x + 12 - 24$
Now let us take the terms having the unknown variable $x$ on one side and others on the other side.
$ \Rightarrow 5x - 4x > 10 - 12$
On simplifying it further we get
$ \Rightarrow x > - 2$
Now we can see that the solution is $ - 2$ .
The given replacement set is $\left\{ { - 4, - 3, - 2, - 1,0,1,2,3,4} \right\}$ the solution we got is $x > - 2$ so the solution set will be $\left\{ { - 1,0,1,2,3,4} \right\}$ .
We are also asked to represent those points in the number so let us first draw the number line.
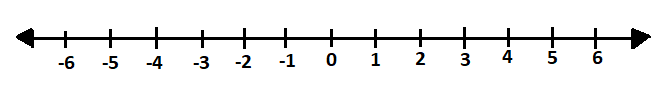
Now let us mark those points in the solution set.

Thus, we have found the solution set and also, we have represented them on the number line.
Note: While solving the inequation we are not supposed to make the inequality a symbol that may lead us to a wrong solution. In this problem, the given equation was an inequality while solving them we didn’t change the inequality sign. Also, we got the solution for x as $x > - 2$ since it is greater than minus two, we got the solution set from $ - 1$ to $4$ as per in the given replacement set. If the solution was greater than or equal to two then we have included the minus two.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




