Question

How do you solve the inequality $2y < y+2$?

Answer 1

Hint: In this problem we have given with an inequality and we need to solve the given inequality. We can observe the given expression that on the both sides of the equation we have the variable $y$. On the left-hand side, we have $2y$ and on the right-hand side we have $y$. So, we will first subtract the $y$ from both sides of the given expression in order to get all the variables are at one side. After subtracting the $y$ from both sides we have observed the solution of the inequality has been obtained.

Complete step by step answer:
Given inequality, $2y < y+2$.
We can observe that the variable $y$ is on both sides of the given expression. On the left-hand side, we have $2y$ and on the right-hand side we have $y$. So, subtracting $y$ from both sides of the above expression, then we will get
$\Rightarrow 2y-y < y+2-y$
Rearranging the terms in the above expression, then we will have
$\Rightarrow 2y-y < y-y+2$
We know that $+a-a=0$, then the above equation is modified as
$\Rightarrow 2y-y < 2$
Taking $y$ as common in the Left-hand side from the above equation, then we will get
$\Rightarrow y\left( 2-1 \right) < 2$
Simplifying the above expression, then we will have
$\Rightarrow y < 2$

Hence the solution of the given inequality $2y < y+2$ is $y < 2$.

Note: We can plot the graph of the given inequality to check whether the obtained solution is correct or wrong. When we plot the given inequality $2y < y+2$ in graph paper, then we will get

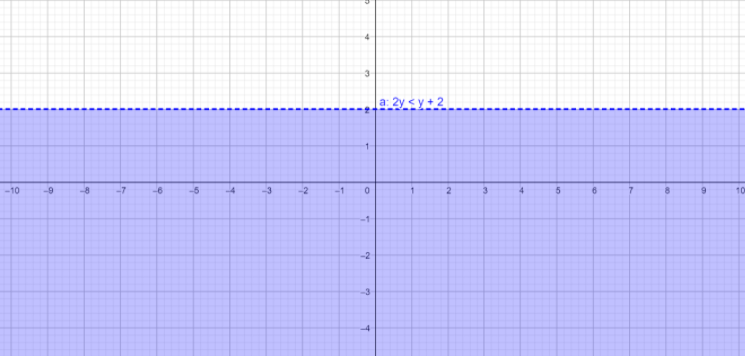
From the above graph also, we can say that the solution of the given inequality $2y < y+2$ is $y < 2$.