Question

How do you solve the graph the absolute value inequality \[\left| 4x+1 \right|\le 5\] ?

Answer 1

Hint: From the question we are given draw a graph from the equation \[\left| 4x+1 \right|\le 5\] . As we know that modulus has two cases we have to solve the two cases and then we will get an equation. Then we have to solve the graph based upon the inequality equation.

Complete step by step solution:
From the given question we are given to solve the graph the absolute value inequality of \[\left| 4x+1 \right|\le 5\] .
Let us consider the given equation as equation (1).
\[\left| 4x+1 \right|\le 5............\left( 1 \right)\]
As we know formula
\[\left| x \right|=\pm x\]
Let us consider the above formula as formula (f1).
\[\left| x \right|=\pm x........\left( f1 \right)\]
From the formula (f1) we have noticed that \[\left| x \right|\] has two cases i.e. positive x and negative x.
Let us consider the first case i.e. positive case for the equation (1), we get
\[\begin{align}
  & \Rightarrow 4x+1\le 5 \\
 & \Rightarrow 4x\le 4 \\
 & \Rightarrow x\le 1 \\
\end{align}\]
Let us consider the above equation as equation (1).
\[x\le 1...........\left( 1 \right)\]
From the second case i.e. negative case for the equation (2), we get
\[\begin{align}
  & \Rightarrow -4x-1\le 5 \\
 & \Rightarrow -4x\le 6 \\
 & \Rightarrow x\ge -\dfrac{6}{4} \\
 & \Rightarrow x\ge -\dfrac{3}{2} \\
\end{align}\]
Let us consider
\[x\ge -\dfrac{3}{2}.........\left( 2 \right)\]
Therefore, from equation (1) and (2).
\[1\ge x\ge -\dfrac{3}{2}\]
Let us consider the above function as equation (3).
\[1\ge x\ge -\dfrac{3}{2}.........\left( 3 \right)\]
By observing the equation (3) we can say that the region of the graph is at limits \[\left( 1,-\dfrac{3}{2} \right)\].
Therefore graph for the given problem is

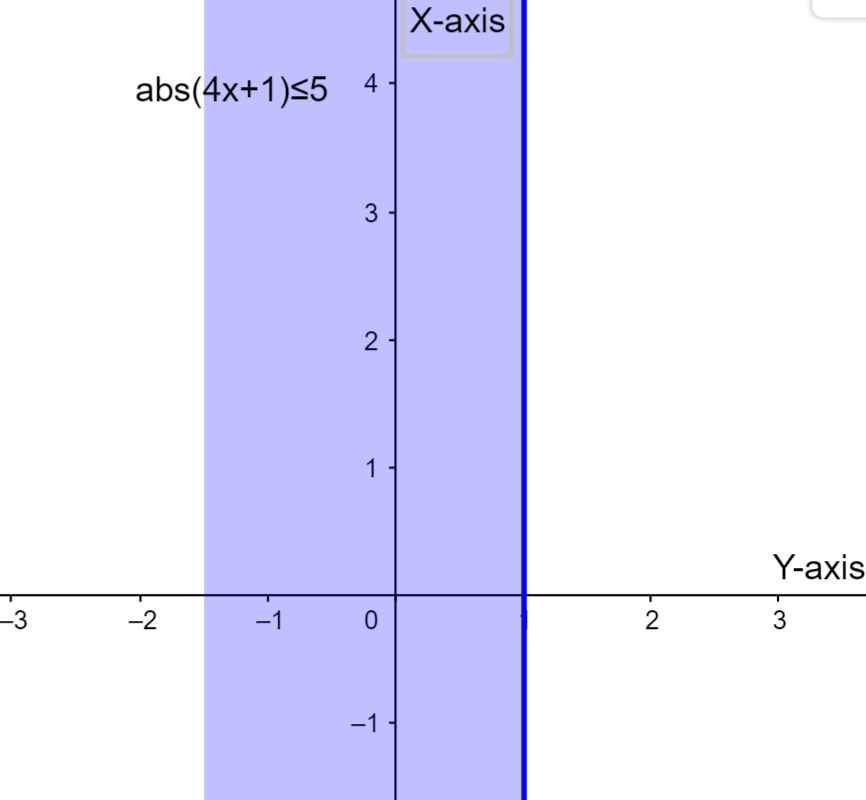
Note: We have to note a point that modulus has two cases while solving the problem. We have to note a point that if we multiply an inequality equation with x then the sign of inequality also changes. We can also do this problem using a number line method which is used to solve these types of problems in competitive exams.