Question

Solve the following system of linear equations graphically: \[2x\text{ }+\text{ }y\text{ }=\text{ }6,\text{ }x\text{ }-\text{ }2y\text{ }+\text{ }2\text{ }=\text{ }0\]
Find the vertices of the triangle formed by the above two lines and the x-axis. Also find the area of the triangle.
a) Vertices of the triangle are A(1, 2), 8(5, 0) and C(-2, 0) and Area: 10 square units
b) Vertices of the triangle are A(4, 2), 8(2, 0) and C(-2, 0) and Area: 15 square units
c) Vertices of the triangle are A(0, 2), 8(1, 0) and C(-2, 0) and Area: 7 square units
d) Vertices of the triangle are A(2, 2), 8(3, 0) and C(-2, 0) and Area: 5 square units

Answer 1

Hint: Find any two points on each line. Then plot them both on a graph, by using this graph you can find the point of intersection. Now find the points where it cuts the x-axis. Now using 3 points find the area of the triangle formed. This area is required as a result of the given question.

Complete step-by-step solution
Given equation in the question, can be written in the form of:
\[x-2y\text{ }+\text{ }2\text{ }=\text{ }0\ldots \ldots \ldots \ldots \ldots \ldots \left( 1 \right);\text{ }2x\text{ }+\text{ }y-\text{ }\text{ }6\text{ }=\text{ }0\ldots \ldots \ldots \ldots \ldots ..\left( 2 \right)\]
The method to draw these straight lines on the graph paper is as follows:
Let us take eq. (1),
\[x-2y\text{ }+\text{ }2\text{ }=\text{ }0\]
Now, put x as 0 in the above equation we get,
$\begin{align}
  & 0-2y+2=0 \\
 & \Rightarrow 2y=2 \\
 & \Rightarrow y=1 \\
\end{align}$
Now, put y as 0 in eq. (1) we get,
$\begin{align}
  & x-2\left( 0 \right)+2=0 \\
 & \Rightarrow x+2=0 \\
 & \Rightarrow x=-2 \\
\end{align}$
Hence, we got two points (0, 1) and (-2, 0).
Now, mark these points on the graph paper and make a line passing through these two points. In this way, we will plot the eq. (1) on the graph paper.
Similarly, we can draw the eq. (2).
\[2x\text{ }+\text{ }y\text{ }-\text{ }6\text{ }=\text{ }0\]
Now, put x as 0 in the above equation we get,
$\begin{align}
  & 0+y-6=0 \\
 & \Rightarrow y=6 \\
\end{align}$
Now, put y as 0 in eq. (2) we get,
$\begin{align}
  & 2x+\left( 0 \right)-6=0 \\
 & \Rightarrow 2x-6=0 \\
 & \Rightarrow 2x=6 \\
 & \Rightarrow x=\dfrac{6}{2}=3 \\
\end{align}$
Hence, we got two points (0, 6) and (3, 0).
Now, plot these points on the graph paper and draw a line passing through these points.
By plotting both the lines, we can get the value of the intersection point:

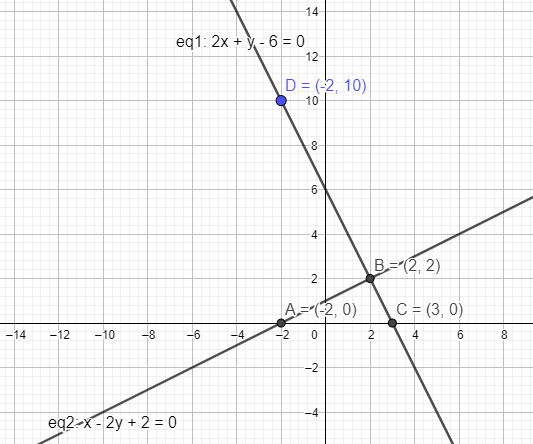
The intersection point of both the lines is given by \[\left( 2,\text{ }2 \right).\] By substituting y = 0 in the equation (2), we get value of x as \[2x\text{ }-\text{ }6\text{ }=\text{ }0.\]
By adding 6 on both sides, we can get value of x as, \[2x\text{ }=\text{ }6\]
By dividing with 2 on both sided, we get the value as,\[x\text{ }=\text{ }3\]
So, the vertices of triangle formed are given as follows:
\[\left( -2,\text{ }0 \right);\text{ }\left( 2,\text{ }2 \right);\text{ }\left( 3,\text{ }0 \right)\]
As it is on the x-axis. The y-coordinate of the middle point is the height of the triangle. Height = 2 units.
As 2 points of base are on x-axis, difference of x-coordinate is base: base \[=\text{ }3-\text{ }\left( -2 \right)\text{ }=\text{ }5\] units.
The area of triangle is given by the formula,
$A=\dfrac{1}{2}\text{base}\times \text{height}$
By substituting their values we get area s value as:
$\text{area=}\dfrac{1}{2}\times 2\times 5=5\text{ square units}\text{.}$
Therefore option (d) is the correct answer for the given question.

Note: While getting the intersection points try to maintain the plot with great accuracy or else you may misplace the point and get the intersection point wrong. Be careful while calculating the points on the x-axis, because they form the base for our triangle. While getting area use the given conditions only when the base is x-axis or the height of the triangle may change its form.