Question

Solve the following simultaneous equations:
4m+3n = 18 and 3m -2n = 5
[a] m = 3 , n = 2
[b] m =-3, n=-2
[c] m=3, n =-2
[d] m = -3, n = 2

Answer 1

Hint: Solve the given system of equations using the elimination method or using the substitution method or graphically. Hence find the value of m and n.

Complete step-by-step answer:
Solving using the elimination method:
We have
4m +3n = 18 (i)
3m-2n =5 (ii)
Multiplying equation (i) by 2 and equation (ii) by 3 and adding , we get
8m + 6n = 36
9m – 6n = 15
Hence 17m = 51
Dividing both sides by 17, we get
$m=\dfrac{51}{17}=3$
Substituting the value of m in equation (i) , we get
$\begin{align}
  & 4\left( 3 \right)+3n=18 \\
 & \Rightarrow 12+3n=18 \\
\end{align}$
Subtracting 12 from both sides, we get
$3n=6$
Dividing both sides by 3, we get
$n=\dfrac{6}{3}=2$
Hence we have m = 3 and n = 2. Hence option [a] is correct.

Note: Alternative method:
Solving using the substitution method:
We have
4m +3n = 18 (i)
3m-2n =5 (ii)
From equation (ii), we have $3m-2n=5$
Adding 2n on both sides, we get
$3m=5+2n$
Dividing both sides by 3, we get
$m=\dfrac{2n+5}{3}\text{ (iii)}$
Substituting the value of m in equation (i), we get
$4\left( \dfrac{2n+5}{3} \right)+3n=18$
Multiplying both sides by 3, we get
$\begin{align}
  & 4\left( 2n+5 \right)+3\left( 3n \right)=54 \\
 & \Rightarrow 8n+20+9n=54 \\
 & \Rightarrow 17n+20=54 \\
\end{align}$
Subtracting 20 from both sides, we get
$17n=54-20=34$
Dividing both sides by 17, we get
$n=\dfrac{34}{17}=2$
Substituting the value of n in equation (iii), we get
$m=\dfrac{2\left( 2 \right)+5}{3}=\dfrac{9}{3}=3$
Hence m = 3 and n = 2
[ii] Plotting the graph:
The graph of the given system is shown below

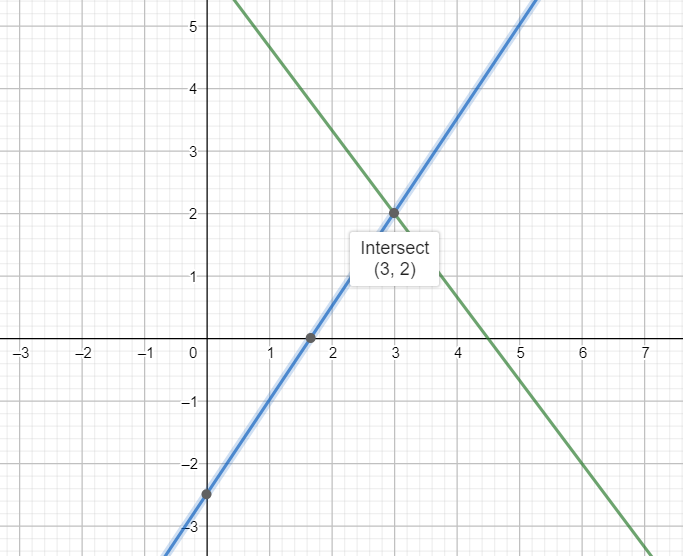
As is evident from the graph, the given system intersects at (3,2)
Hence m = 3 and n= 2.