Question

Solve the following question given below:
If the bisector of the exterior vertical angle of a triangle be parallel to the base, then show that the triangle is isosceles.

Answer 1

Hint: Take a standard base of the triangle, then bisect the opposite exterior angle so that the bisector is parallel to the base. Then join the bisector with the edge to complete another triangle. Use congruence of triangles to prove that the two sides are equal and hence isosceles.

Complete step-by-step solution:
Let us take a triangle, \[\vartriangle ABC\] as shown in the figure below.
Let us consider \[BC\] as the base of the triangle.
The bisector of the exterior angle \[A\] is extended to \[D\] and the point \[D\] is joined to \[C\] to complete another triangle as shown in the figure given below:

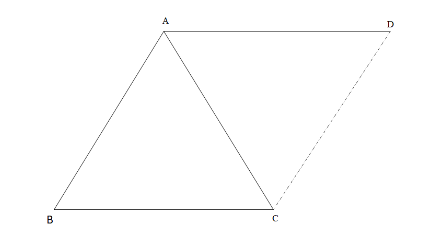
In \[\vartriangle ABC\] and \[\vartriangle ADC\],
\[AD\left\| {BC} \right.\] which is given to us in the question:
There are a pair of alternate angles which are formed from the parallel line.
\[ \Rightarrow \angle ACB = \angle CAD\]
The other pair formed from the parallel lines; we have;
\[\angle BAC = \angle ACD\]
Then we have the single side common to both the triangles;
\[AC = AC\]
Therefore, by ASA congruence,
We have,
\[AB = AC\]
Hence, two sides are equal.
$\therefore $ The triangle is isosceles.

Note: We have to remember that in geometry an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bi-pyramids and certain Catalan solids.
We have to use the axioms. There are four axioms. ASA, SSS, ASS, RHS axioms. In a triangle, we have to choose the required sides or angles so that they fit in one axiom. After we prove the congruence of triangles, we get another two sides as equal or any angle as equal which completes the solution about proving the given question.