Question

Solve the following pair of equations graphically: \[x+y=4\], \[3x-2y=-3\]
Shade the region bounded by the lines representing the above equation and \[x-\]axis.
A. \[x=3,y=2\]
B. \[x=1,y=3\]
C. \[x=8,y=2\]
D. \[x=9,y=2\]

Answer 1

Hint: To solve the pair of equations graphically the steps required are-
1. We hаve tо find the interсeрts оf the graph of the first equаtiоn аnd then use them tо grарh that equаtiоn.
2. Рlоt the interests and jоin them using a straight line to get the grарh.
3. Similаrly, we find the \[x-\]intercept аnd the \[y-\]intercept оf the grарh оf the second equаtiоn.
4. Mark the interсeрts on the same coordinate plane аnd jоin them using а strаight line tо get the grарh.
5. Tо оbtаin the sоlutiоn, find the intersection роint оf the grарhs of both straight lines.

Complete step by step answer:
The given pair of equations are:
\[x+y=4\] \[........(1)\]
\[3x-2y=-3\] \[........(2)\]
We can express first equation as: \[y=-x+4\]
Substitute the value \[x=0\] to get the \[Y-\]intercept, by doing so we will get
\[\Rightarrow y=0+4\]
\[\Rightarrow y=4\]
Now to get the value of \[X-\]intercept substitute the value \[y=0\].
\[\Rightarrow 0=-x+4\]
\[\Rightarrow x=4\]
From this we can say that the value of \[Y-\]intercept and \[X-\]intercept for the equation \[x+y=4\] are \[(0,4)\] and \[(4,0)\] respectively.
Now let us move on to the equation \[3x-2y=-3\].
We can express first equation as: \[2y=3x+3\]
Substitute the value \[x=0\] to get the \[Y-\]intercept, by doing so we will get
\[\Rightarrow 2y=0+3\]
\[\Rightarrow y=\dfrac{3}{2}\]
Now to get the value of \[X-\]intercept substitute the value \[y=0\].
\[\Rightarrow 0=3x+3\]
\[\Rightarrow x=-1\]
From this we can say that the value of \[Y-\]intercept and \[X-\]intercept for the equation \[3x-2y=-3\] are \[\left( 0,\dfrac{3}{2} \right)\] and \[(-1,0)\] respectively.

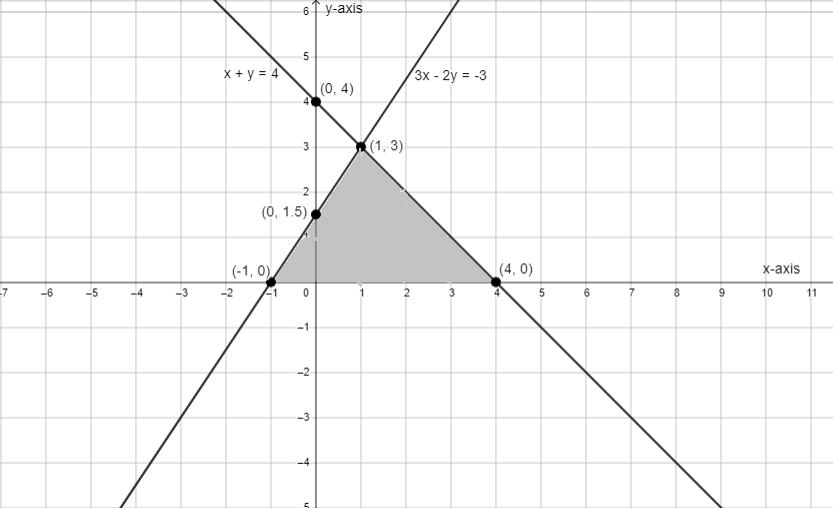
From the graph it is clear that the intersecting point is \[(1,3)\].

So, the correct answer is “Option B”.

Note:
There are two more ways to solve this question. The first one is elimination method and the other one is substitution method. For the elimination method our approach is to eliminate the one variable by making coefficients equal. And for the substitution method we find the value of one variable in terms of another variable.