Question

Solve the following linear programming problem graphically:
Maximize: Z = 60x + 40y
Subject to the constraints:
x + 2y $ \leqslant $ 12, 2x + y $ \leqslant $ 12, x + (5/4) y $ \geqslant $ 5, x $ \geqslant $ 0, and y $ \geqslant $ 0

Answer 1

Hint: In this particular question plot all the constraints on a graph and mark the common region then mark all the points of intersection in this region then substitute these points one by one in the equation which we have to maximize so use these concepts to reach the solution of the question.

Complete step-by-step answer:

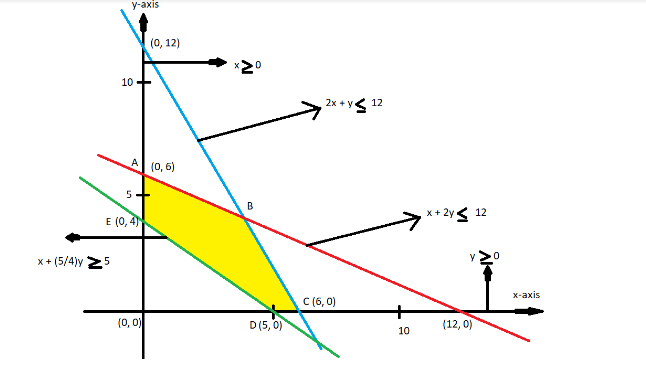
Given equation which we have to maximize
Maximize: Z = 60x + 40y................... (1)
Now the constraints are
x + 2y $ \leqslant $ 12, 2x + y $ \leqslant $ 12, x + (5/4) y $ \geqslant $ 5, x $ \geqslant $ 0, and y $ \geqslant $ 0
Now plot these lines on a graph.
So, x + 2y $ \leqslant $ 12
Now calculate x and y axis coordinates so that we can plot this easily.
So for x coordinate substitute y = 0 we have,
 $ \Rightarrow x + 0 \leqslant 12 $
 $ \Rightarrow x \leqslant 12 $
So point on x-axis is (12, 0)
Now for y coordinate substitute x = 0 we have,
 $ \Rightarrow 0 + 2y \leqslant 12 $
 $ \Rightarrow y \leqslant 6 $
So point on y-axis is (0, 6)
So join these points as shown in the figure.
Now plot 2x + y $ \leqslant $ 12
Now calculate x and y axis coordinates so that we can plot this easily.
So for x coordinate substitute y = 0 we have,
 $ \Rightarrow 2x + 0 \leqslant 12 $
 $ \Rightarrow x \leqslant 6 $
So point on x-axis is (6, 0)
Now for y coordinate substitute x = 0 we have,
 $ \Rightarrow 0 + y \leqslant 12 $
 $ \Rightarrow y \leqslant 12 $
So point on y-axis is (0, 12)
So join these points as shown in the figure.
Now plot x + (5/4) y $ \geqslant $ 5 we have,
Now calculate x and y axis coordinates so that we can plot this easily.
So for x coordinate substitute y = 0 we have,
 $ \Rightarrow x + 0 \geqslant 5 $
 $ \Rightarrow x \geqslant 5 $
So point on x-axis is (5, 0)
Now for y coordinate substitute x = 0 we have,
 $ \Rightarrow 0 + \dfrac{5}{4}y \leqslant 5 $
 $ \Rightarrow y \leqslant 4 $
So point on y-axis is (0, 4)
So join these points as shown in the figure.
Now, x $ \geqslant $ 0, and y $ \geqslant $ 0 are the regions positive side of y-axis and positive side of x-axis respectively as shown in the graph.
Now the common region is marked with yellow color.
So ABCDE is the common region of these lines.
Now find the coordinates of point B.
As point B is the intersection of lines x + 2y = 12 and 2x + y = 12
So multiply by 2 in second equation and subtract from first we have,
 $ \Rightarrow x + 2y - 2\left( {2x + y} \right) = 12 - 2\left( {12} \right) $
 $ \Rightarrow - 3x = - 12 $
 $ \Rightarrow x = 4 $
Now put this value in any above equation so we have,
 $ \Rightarrow 4 + 2y = 12 $
 $ \Rightarrow 2y = 8 $
 $ \Rightarrow y = 4 $
So the coordinates of point B is (4, 4).
Now find out the value of z at these points we have,
At point A (0, 6)
 $ \Rightarrow Z = 60\left( 0 \right) + 40\left( 6 \right) = 240 $
At point B (4, 4)
 $ \Rightarrow Z = 60\left( 4 \right) + 40\left( 4 \right) = 240 + 240 = 480 $
At point C (6, 0)
 $ \Rightarrow Z = 60\left( 6 \right) + 40\left( 0 \right) = 360 $
At point D (5, 0)
 $ \Rightarrow Z = 60\left( 5 \right) + 40\left( 0 \right) = 300 $
At point E (0, 4)
 $ \Rightarrow Z = 60\left( 0 \right) + 40\left( 4 \right) = 160 $
So as we see that the maximum value of z is at point C (4, 4) and the maximum value of z is 480.
So this is the required answer.

Note: Whenever we face such types of questions the key concept we have to remember is that to maximize the function graphically first we have to find out the common region of the given equations than mark all boundary points as above we marked then evaluate the value of z at all these points as above calculated then check at which point Z is maximized, so at this particular point the value of z is the required answer.