Question

Solve the following inequation and write the solution set :
$13x - 5 < 15x + 4 < 7x + 12,x \in R$
Represent the solution on a real number line.

Answer 1

Hint: A linear equation resembles another equation. it's far composed of expressions which are set identical to every other. We will consider two inequalities out of three at once and solve the inequalities for the value $x$ . We will get a range of values of x from those two equations. Then we just need to find the common region or the intersection of these two regions which will be our final answer.

Complete step-by-step answer:
The given inequalities are:
$13x - 5 < 15x + 4 < 7x + 12,x \in R$
Now we will consider two inequalities at once,
$15x + 4 > 13x - 5$ and $15x + 4 < 7x + 12$
Rearranging the terms of the inequalities and solving the inequalities for the value of $x$,
$15x - 13x > - 5 - 4$ and $15x - 7x < 12 - 4$
$2x > - 9$ and $8x < 8$
$x > \dfrac{{ - 9}}{2}$ and $x < \dfrac{8}{8}$
$x > \dfrac{{ - 9}}{2}$ and $x < 1$
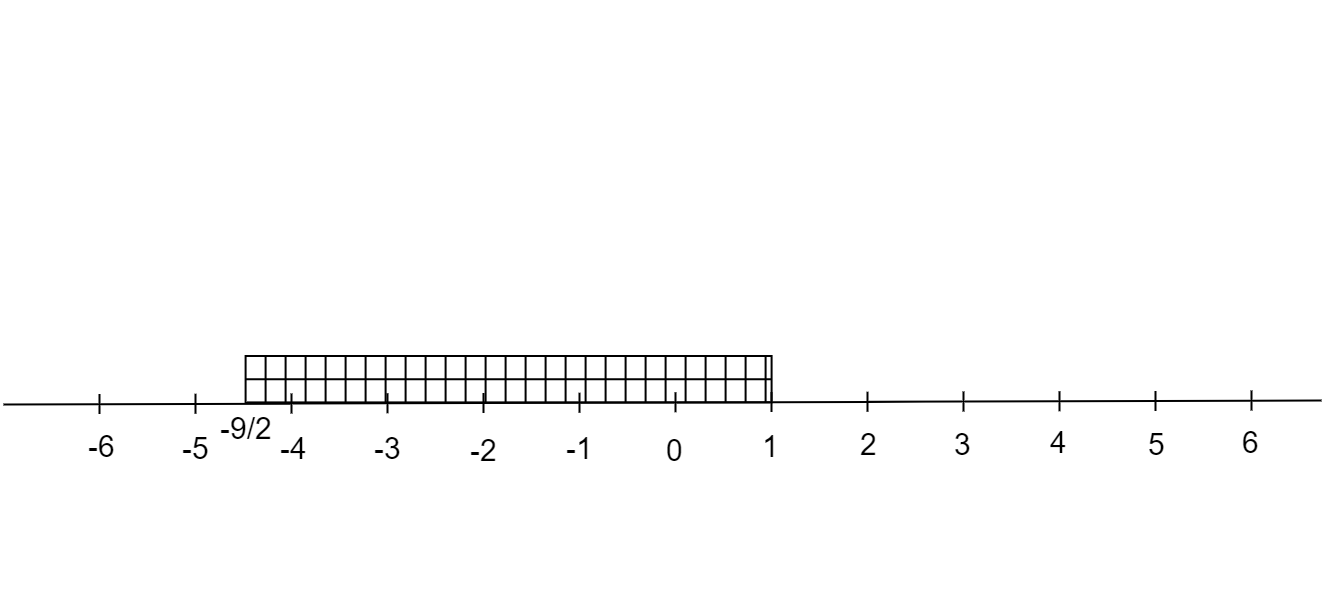
The range of $x:\dfrac{{ - 9}}{2} < x < 1,x \in R$
The real number line for the range of $x$ is

Note: Linear Inequations- Mathematical expressions assist us to convert trouble statements into entities and for that reason, help resolve them. If the expression equates to two expressions or values, then its miles are referred to as an equation. For e.g.,$3x + 5y = 8$ then again, if an expression relates two expressions or values with a ‘$ < $’ (less than) sign, ‘$ > $’ (extra than) signal, ‘$ \leqslant $’ (less than or identical) signal or ‘$ \geqslant $’ (greater than or identical) signal, then it's far referred to as an Inequality. An inequality that involves a linear characteristic is a linear inequality. It seems like a linear equation, besides that the ‘$ = $’ signal is replaced through an inequality sign, known as linear inequations.