
Solve the following equations graphically for x and y.
$4x+3y-7=0$ and
$2x-3y+1=0$
Answer
604.5k+ views
Hint: In this given question, we should first construct the straight lines with the given equations on the Cartesian plane, then, we can find common solutions for x and y as the coordinates of the point of intersection of these two constructed lines. It is because the point of intersection belongs to both the lines and hence satisfies both the equations. To construct the straight lines, we have to assume values of x and find corresponding values of y for both the given lines.
Complete step-by-step answer:
We are given to solve the equation $4x+3y-7=0$ and $2x-3y+1=0$ by using graphical method.
In order to solve this question, first of all we must construct the two lines of the given two equations. The point of intersection which lies in both the lines will be a solution to both the lines.
In order to draw a line of a given equation, we need to have at least two points whose coordinates satisfy the equation.
The process of solving is as follows:
The first equation is $4x+3y-7=0$
So, putting different values of x in the above equation and obtaining the corresponding value of y, we get
If x=0, $y=\dfrac{7}{3}$
If x=1, y=1 and
If x=2, $y=\dfrac{-1}{3}$
The graph of the line is:
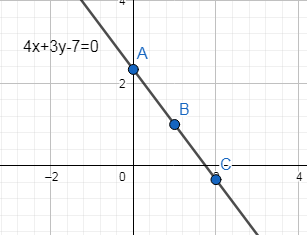
The second equation is $2x-3y+1=0$
So, putting different values of x in the above equation and obtaining the corresponding value of y, we get
If x=0, $y=\dfrac{1}{3}$
If x=1, y=1 and
If $x=\dfrac{-1}{2}$ , y=0
The graph of the second line is plotted on the same graph as:
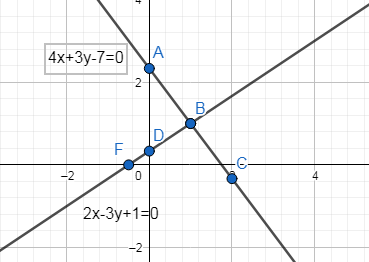
As, we can see the point of intersection is (1,1) and it belongs to both the drawn lines. So, the value of x is 1 and the value of y is 1 for which both the equations are satisfied.
Therefore, we have solved the given question by graphical method.
Note: Here, as the equations are linear in two variables, only two points can satisfy to form a line but still we have taken a third point in order to verify and assure the correctness of our solution. However, for equations having higher number of variables, we must take the number of points equal to the number of variables to get the corresponding graphs.
Complete step-by-step answer:
We are given to solve the equation $4x+3y-7=0$ and $2x-3y+1=0$ by using graphical method.
In order to solve this question, first of all we must construct the two lines of the given two equations. The point of intersection which lies in both the lines will be a solution to both the lines.
In order to draw a line of a given equation, we need to have at least two points whose coordinates satisfy the equation.
The process of solving is as follows:
The first equation is $4x+3y-7=0$
So, putting different values of x in the above equation and obtaining the corresponding value of y, we get
If x=0, $y=\dfrac{7}{3}$
If x=1, y=1 and
If x=2, $y=\dfrac{-1}{3}$
| x | 0 | 1 | 2 |
| y | $\dfrac{7}{3}$ | 1 | $\dfrac{-1}{3}$ |
The graph of the line is:

The second equation is $2x-3y+1=0$
So, putting different values of x in the above equation and obtaining the corresponding value of y, we get
If x=0, $y=\dfrac{1}{3}$
If x=1, y=1 and
If $x=\dfrac{-1}{2}$ , y=0
| x | 0 | 1 | $\dfrac{-1}{2}$ |
| y | $\dfrac{1}{3}$ | 1 | 0 |
The graph of the second line is plotted on the same graph as:

As, we can see the point of intersection is (1,1) and it belongs to both the drawn lines. So, the value of x is 1 and the value of y is 1 for which both the equations are satisfied.
Therefore, we have solved the given question by graphical method.
Note: Here, as the equations are linear in two variables, only two points can satisfy to form a line but still we have taken a third point in order to verify and assure the correctness of our solution. However, for equations having higher number of variables, we must take the number of points equal to the number of variables to get the corresponding graphs.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




