
Solve the following equations:
$\begin{align}
& 1.\text{ }x-2=7 \\
& 2.\text{ }y+3=10 \\
\end{align}$
Answer
611.1k+ views
Hint: For solving this problem as we have two linear equations in terms of two unknown variables and as in both equations there is only one variable for example in $x-2=7$ coefficient of $y$ is zero so, we will solve them directly to find the value of unknown variables. After that, we will plot them on the graph and verify our answer.
Complete step by step answer:
Given:
We have two linear equations $x-2=7$ , $y+3=10$ and we have to find the value of $x$ and $y$ .
Now, the given equations are:
$\begin{align}
& x-2=7...........\left( 1 \right) \\
& y+3=10............\left( 2 \right) \\
\end{align}$
Now, we can directly solve them and find the value of $x$ and $y$ . Then,
$\begin{align}
& x-2=7 \\
& \Rightarrow x=7+2 \\
& \Rightarrow x=9 \\
& y+3=10 \\
& \Rightarrow y=10-3 \\
& \Rightarrow y=7 \\
\end{align}$
Now, from the above results we can say that if $x-2=7$ and $y+3=10$ then, the value of $x=9$ and value of $y=7$ . For more clarity, we can also plot both given equations on the x-y plane and verify whether they are intersecting at point (6,3) or not. The plot is shown below:
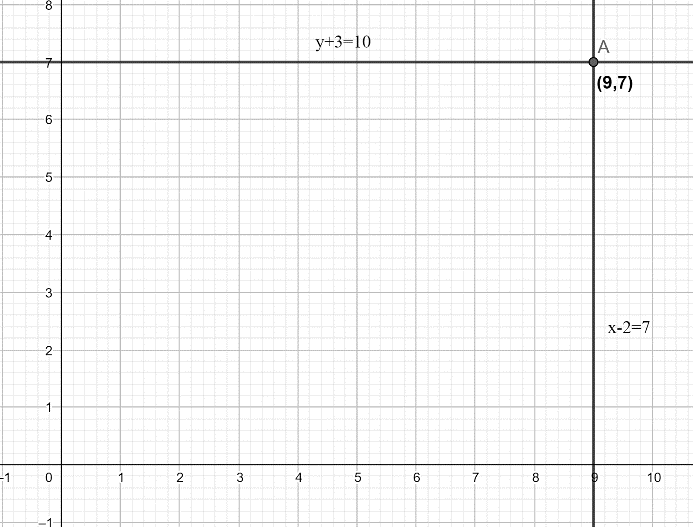
Now, from the above figure, we can verify that the given two equations of straight lines will intersect at the point whose $x$ coordinate will be $x=9$ and $y$ coordinate will be $y=7$ .
Hence, if $x-2=7$ and $y+3=10$ then, the value of $x=9$ and value of $y=7$ .
Note: Here, the student should simply do the substitution correctly and though the problem is very easy, we should avoid calculation mistakes while solving. Moreover, in such questions, once we solve the equations then, we should verify it from graphs for better understanding.
Complete step by step answer:
Given:
We have two linear equations $x-2=7$ , $y+3=10$ and we have to find the value of $x$ and $y$ .
Now, the given equations are:
$\begin{align}
& x-2=7...........\left( 1 \right) \\
& y+3=10............\left( 2 \right) \\
\end{align}$
Now, we can directly solve them and find the value of $x$ and $y$ . Then,
$\begin{align}
& x-2=7 \\
& \Rightarrow x=7+2 \\
& \Rightarrow x=9 \\
& y+3=10 \\
& \Rightarrow y=10-3 \\
& \Rightarrow y=7 \\
\end{align}$
Now, from the above results we can say that if $x-2=7$ and $y+3=10$ then, the value of $x=9$ and value of $y=7$ . For more clarity, we can also plot both given equations on the x-y plane and verify whether they are intersecting at point (6,3) or not. The plot is shown below:
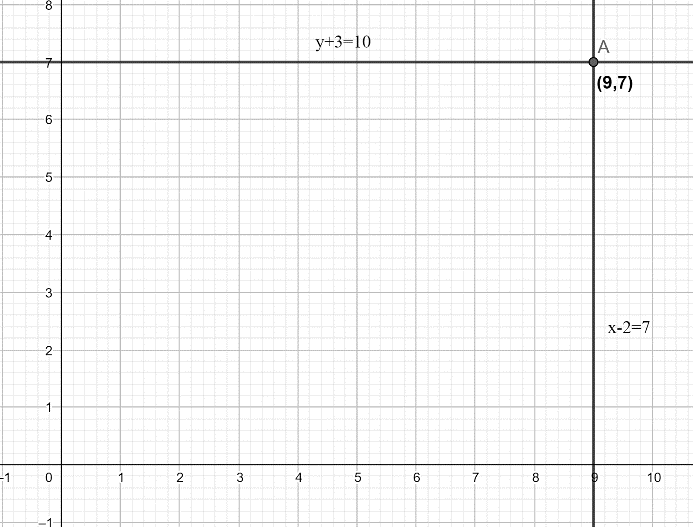
Now, from the above figure, we can verify that the given two equations of straight lines will intersect at the point whose $x$ coordinate will be $x=9$ and $y$ coordinate will be $y=7$ .
Hence, if $x-2=7$ and $y+3=10$ then, the value of $x=9$ and value of $y=7$ .
Note: Here, the student should simply do the substitution correctly and though the problem is very easy, we should avoid calculation mistakes while solving. Moreover, in such questions, once we solve the equations then, we should verify it from graphs for better understanding.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




