Question

Solve the following equation and represent the solution set on the number line. $-3<-\dfrac{1}{2}-\dfrac{2x}{3}\le \dfrac{5}{6},x\in R$.

Answer 1

Hint: For solving this question you should know about the number line and how to represent values on it. In this problem first we will find the value of $x$ and then we will represent them on the number line.

Complete step by step answer:
According to the question, it is asked to us to solve the following equation and represent a solution set on the number line. The equation given is: $-3<-\dfrac{1}{2}-\dfrac{2x}{3}\le \dfrac{5}{6},x\in R$. So, here we know that we can’t solve this directly in this form. We have to convert this in the integer form which is provided in fractional form already. So, for this we will multiply the whole equation by 6.
So, multiply the whole equation by 6.
$\begin{align}
  & \Rightarrow -18\le -\dfrac{1}{2}\times 6-\dfrac{2x}{3}\times 6\le \dfrac{5}{6}\times 6 \\
 & \Rightarrow -18\le -3-4x\le 5 \\
\end{align}$
We can write it as,
$-15\le -4x\le 8\ldots \ldots \ldots \left( i \right)$
Now for getting the value of $x$ we have to divide it again by -4.
So, by dividing the equation (i) by -4,
$\begin{align}
  & \Rightarrow \dfrac{-15}{-4}\ge x \ge \dfrac{8}{-4} \\
 & \Rightarrow \dfrac{15}{4}\ge x \ge -2 \\
 & \Rightarrow -2\le x \le \dfrac{15}{4} \\
\end{align}$
So, this,
$\Rightarrow x\in \left[ -2,\dfrac{15}{4} \right]$
So, if we represent this on the number line, we will get as follows:

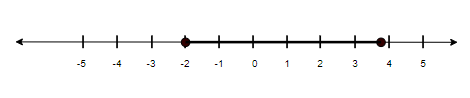
This is the number line representation of this.

Note: While solving these types of questions you have to keep in mind that always try to make all the numbers in integer form, because to show an integer on the number line is much easier than decimal or fractional form. And this representation can be exact or not because everything depends on the scale which we are using.