Question

How do you solve the equation $ - {x^2} - 7x = 0$ by graphing?

Answer 1

Hint: This problem deals with the conic sections. A conic section is a curve obtained as the intersection of the surface of a cone with a plane. There are three such types of conic sections which are, the parabola, the hyperbola and the ellipse. This problem is regarding one of those conic sections, which is a parabola. The general form of an equation of a parabola is given by ${x^2} = - 4ay$.

Complete step-by-step answer:
The given equation is $ - {x^2} - 7x = 0$, the graph of the given equation can be obtained.
Let $y = - {x^2} - 7x$
Here to get the solutions of $x$, in the above equation put $y = 0$.
$ \Rightarrow - {x^2} - 7x = 0$
Now take the variable $ - x$ common in the above equation:
$ \Rightarrow - x\left( {x + 7} \right) = 0$
Here $x = 0$ and $x + 7 = 0$, hence $x = - 7$.
The solutions of $x$ are $x = 0$ and $x = - 7$.
So the points $\left( {0,0} \right)$ and $\left( { - 7,0} \right)$ are on the graph.
The equation of the curve looks like a parabola, a parabola has a vertex.
If the parabola is given by $y = a{x^2} + bx + c$, then the x-coordinate of the vertex is given by:
$ \Rightarrow x = \dfrac{{ - b}}{{2a}}$
Here in the given parabola equation $y = - {x^2} - 7x$, here $a = - 1,b = - 7$.
Now finding the x-coordinate of the vertex:
$ \Rightarrow x = \dfrac{{ - \left( { - 7} \right)}}{{2\left( { - 1} \right)}}$
$ \Rightarrow x = \dfrac{{ - 7}}{2}$
Now to get the y-coordinate of the vertex of the parabola, substitute the value of $x = \dfrac{{ - 7}}{2}$, in the parabola equation, as shown below:
$ \Rightarrow y = - {x^2} - 7x$
$ \Rightarrow y = - {\left( {\dfrac{{ - 7}}{2}} \right)^2} - 7\left( {\dfrac{{ - 7}}{2}} \right)$
Simplifying the above equation, as given below:
$ \Rightarrow y = - \dfrac{{49}}{4} + \dfrac{{49}}{2}$
$ \Rightarrow y = \dfrac{{49}}{4}$
So the vertex of the parabola $y = - {x^2} - 7x$ is A, which is given by:
$ \Rightarrow A = \left( {\dfrac{{ - 7}}{2},\dfrac{{49}}{4}} \right)$
This parabola has its axis parallel to y-axis.
So the graph will be bending at the vertex and crossing the x-axis at $\left( {0,0} \right)$ and $\left( { - 7,0} \right)$.
The graph is shown below:

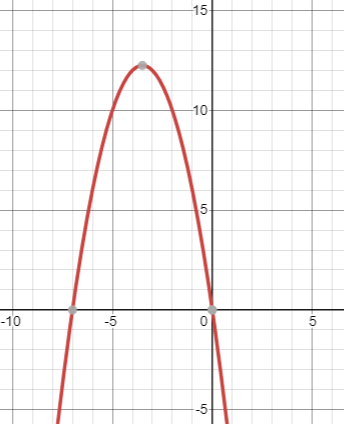
Note:
Please note that if the given parabola is \[{x^2} = - 4ay\], then the vertex of this parabola is the origin $\left( {0,0} \right)$, and there is no intercept for this parabola as there are no terms of x or y. If the equation of the parabola includes any terms of linear x or y, then the vertex of the parabola is not the origin, the vertex has to be found out by simplifying it into its particular standard form.