Question

How do you solve the equation $ {x^2} - 3x = 0 $ by graphing?

Answer 1

Hint: Since one can solve the given equation simply by factoring but in this question it has been asked that you have to solve this graphically. So what you have to do is, first replace the term zero in the equation with $ y $ and then plot the graph of the given equation, after plotting the graph see in which point of abscissa the graph is touch the it, in other words find the value of $ x $ where the graph is touching x-axis or the line $ y = 0 $ , that will be the required solution.

Complete step-by-step answer:
In order to solve the given equation graphically, we have to first simplify the equation by replacing zero with $ y $ as follows
 $ {x^2} - 3x = y $
We can also write it as
 $ y = {x^2} - 3x $
Now, it’s time to plot the graph of the simplified equation, the graph of the simplified equation will look like this:

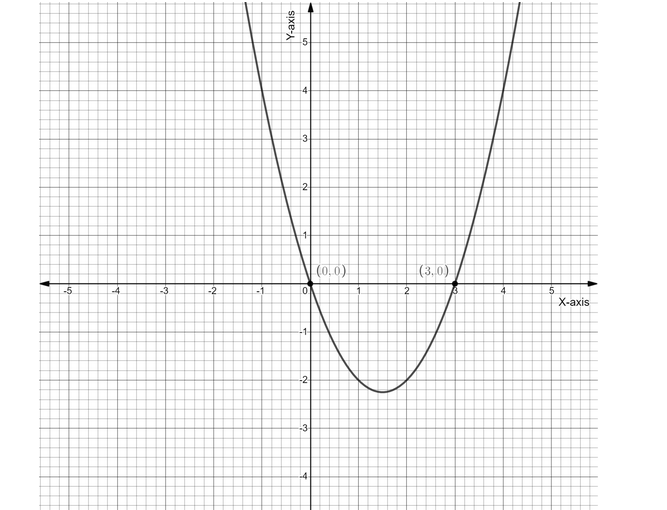
Since we have plotted the graph of the simplified equation, now we will find out the point in the graph which is touching the x-axis or the line $ y = 0 $
So we can see that, at $ x = 0\;{\text{and}}\;x = 3 $ the graph is crossing or touching the x-axis
Therefore $ x = 0\;{\text{and}}\;x = 3 $ are the required solutions of the given equation.

Note: We have got two solutions of the given equation because the equation is of two degrees and also if you find its determinant then you will get a positive number which shows that the equation will have two real and distinct solutions. Also we have found the solution at $ y = 0 $ because when we normally solve any equation then we are also finding $ y = 0 $ at that time too.