Question

How do you solve the equation \[{x^2} - 2x - 24 = 0\] by graphing?

Answer 1

Hint: Here, we will first find the \[x\] and \[y\] intercepts and the vertex to plot the graph of this equation. As this is a quadratic equation, its graph will be U-shaped. After plotting the graph, we will observe what are the possible values of \[x\] when \[y = 0\] to find the required solution using the graph.

Complete step-by-step answer:
The given quadratic equation is: \[{x^2} - 2x - 24 = 0\]
Now, in order to plot a graph of this equation, we will, first of all, determine the \[y\] intercept.
Hence, we will substitute \[x = 0\]
Hence, \[y = f\left( 0 \right) = {\left( 0 \right)^2} - 2\left( 0 \right) - 24 = - 24\]
Thus, the \[y\] intercept is \[\left( {0, - 24} \right)\]
Now, we will determine the \[x\] intercept, by substituting \[y = f\left( x \right) = 0\]
\[{x^2} - 2x - 24 = 0\]
Doing middle term split, we get
\[ \Rightarrow {x^2} - 6x + 4x - 24 = 0\]
\[ \Rightarrow x\left( {x - 6} \right) + 4\left( {x - 6} \right) = 0\]
Factoring out common terms, we get
\[ \Rightarrow \left( {x + 4} \right)\left( {x - 6} \right) = 0\]
By using zero product property, we get
\[\begin{array}{l} \Rightarrow \left( {x + 4} \right) = 0\\ \Rightarrow x = - 4\end{array}\]
Or
\[\begin{array}{l} \Rightarrow \left( {x - 6} \right) = 0\\ \Rightarrow x = 6\end{array}\]
Therefore, for \[y = 0\], we get two \[x\] intercepts, i.e. \[\left( { - 4,0} \right)\] and \[\left( {6,0} \right)\]
Now, we will determine the vertex by using the formula \[x = \dfrac{{ - b}}{{2a}}\] to find the \[x\]-value of the vertex and then, we will substitute this value in the function to find the corresponding value of \[y\].
In the given equation, \[{x^2} - 2x - 24 = 0\] by comparing it to \[a{x^2} + bx + c = 0\], we get,
\[a = 1\], \[b = - 2\] and \[c = - 24\]
Thus, substituting these values in \[x = \dfrac{{ - b}}{{2a}}\], we get,
\[x = \dfrac{{ - \left( { - 2} \right)}}{{2\left( 1 \right)}} = \dfrac{2}{2} = 1\]
Substituting this is the equation \[y = {x^2} - 2x - 24\], we get,
\[y = {1^2} - 2\left( 1 \right) - 24\]
Simplifying the expression, we get
\[ \Rightarrow y = 1 - 2 - 24 = - 25\]
Therefore, the vertex is: \[\left( {1, - 25} \right)\]
Also, let us substitute \[x = 2\] in the \[y = {x^2} - 2x - 24\] thus, we get,
\[y = {2^2} - 2\left( 2 \right) - 24\]
Simplifying the expression, we get
\[ \Rightarrow y = 4 - 4 - 24 = - 24\]
Therefore, the other point is \[\left( {2, - 24} \right)\]
Hence, we will plot the graph having:
\[y\] intercept as \[\left( {0, - 24} \right)\]
\[x\] intercepts as \[\left( { - 4,0} \right)\] and \[\left( {6,0} \right)\]
Vertex: \[\left( {1, - 25} \right)\]
Extra point: \[\left( {2, - 24} \right)\]

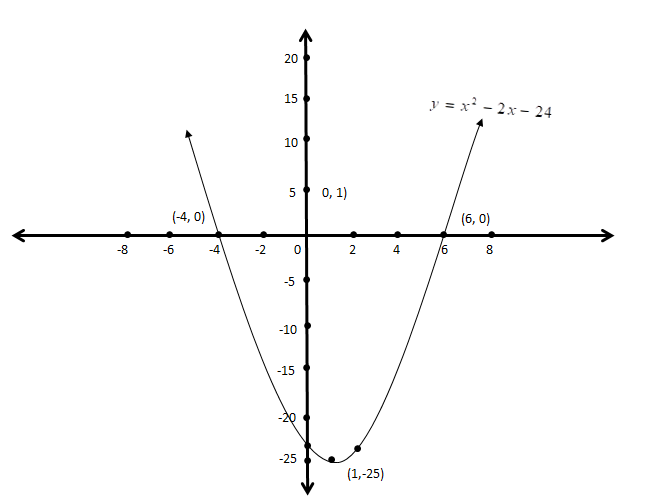
Hence, from this graph, we can clearly observe that the values \[x = - 4\]and \[x = 6\] when \[y = 0\]

Therefore, this is the required solution of the given equation \[{x^2} - 2x - 24 = 0\] by graphing.
Hence, this is the required answer.

Note:
An equation is called a quadratic equation if it can be written in the form of \[a{x^2} + bx + c = 0\] where \[a,b,c\] are real numbers and \[a \ne 0\] , as it is the coefficient of \[{x^2}\] and it determines that this is a quadratic equation. Also, the power of a quadratic equation will be 2 as it is a ‘quadratic equation’. Also, a quadratic equation will give us two roots and its graph is U-shaped as we can observe from this question.