
Solve the equation graphically: x + 3y = 6 and 2x + 3y = 12.
Answer
599.4k+ views
Hint: In order to find the solution to this question, we will find a couple of coordinates for both the equations which will satisfy the equality, and then we will plot the point on the graph and extend them until they intersect each other. Whatever the point will be for the intersection of both the lines will be the solution for the given pair of equations.
Complete step-by-step solution -
In this question, we have been given a pair of equations that is $x + 3y = 6$ and $2x + 3y = 12$ and we have been asked to find the solution of the equations. To solve this question, we will first find the couple of points for both the equation by hit and trial. So, we get,
For equation $x + 3y = 6$,
At $x = 0$,
$0 + 3y = 6$
$y = 2$
At y = 0,
$x + 3(0) = 6$
$x = 6$
At y = 1,
$x + 3(1) = 6$
$x = 3$
So, we can say, for $x + 3y = 6$, we get,
Or we can say (6, 0), (3, 1), (0, 2) are the points which satisfy $x + 3y = 6$.
Similarly, we will find the points for the equation $2x + 3y = 12$. We will get,
At x = 0,
$2(0) + 3y = 12$
$y = 4$
At y = 0,
$2(x) + 3(0) = 12$
$x = 6$
At y = 2,
$2x + 3(2) = 12$
$x = 3$
So, we can say, for $2x + 3y = 12$, we get,
Or we can say (6, 0), (3, 2), (0, 4) are the points which satisfy $2x + 3y = 12$.
Now, we will use these points to plot on the graph and represent the pair of equations. So, we get,
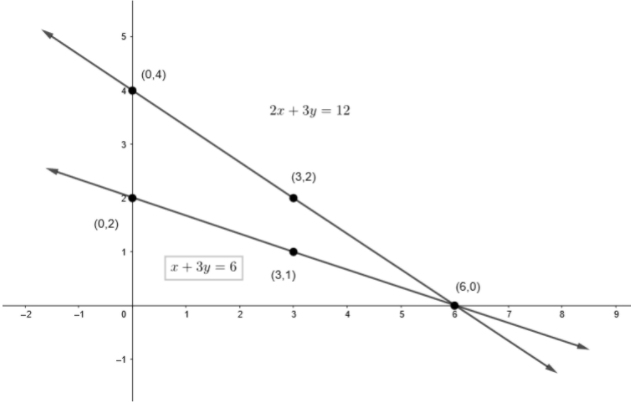
Now, we can see that the pair of lines meet each other at (6, 0). So, we can say that (6, 0) is the answer of $x + 3y = 6$ and $2x + 3y = 12$.
Note: While solving the question, we can verify our answer by putting x and y coordinates in both the equation, and if coordinates satisfy both the equation then our answer is correct otherwise we have to find the answer again. Some points to be kept in mind while plotting lines are to use values of x = 0, 1, -1, 2, -2 instead of using bigger numbers to find corresponding values of y for plotting the graph; if at any point value of y comes out as a fraction, try to look for different values of x such that plotting becomes easier.
Complete step-by-step solution -
In this question, we have been given a pair of equations that is $x + 3y = 6$ and $2x + 3y = 12$ and we have been asked to find the solution of the equations. To solve this question, we will first find the couple of points for both the equation by hit and trial. So, we get,
For equation $x + 3y = 6$,
At $x = 0$,
$0 + 3y = 6$
$y = 2$
At y = 0,
$x + 3(0) = 6$
$x = 6$
At y = 1,
$x + 3(1) = 6$
$x = 3$
So, we can say, for $x + 3y = 6$, we get,
| x | 6 | 3 | 0 |
| y | 0 | 1 | 2 |
Or we can say (6, 0), (3, 1), (0, 2) are the points which satisfy $x + 3y = 6$.
Similarly, we will find the points for the equation $2x + 3y = 12$. We will get,
At x = 0,
$2(0) + 3y = 12$
$y = 4$
At y = 0,
$2(x) + 3(0) = 12$
$x = 6$
At y = 2,
$2x + 3(2) = 12$
$x = 3$
So, we can say, for $2x + 3y = 12$, we get,
| x | 6 | 3 | 0 |
| y | 0 | 2 | 4 |
Or we can say (6, 0), (3, 2), (0, 4) are the points which satisfy $2x + 3y = 12$.
Now, we will use these points to plot on the graph and represent the pair of equations. So, we get,

Now, we can see that the pair of lines meet each other at (6, 0). So, we can say that (6, 0) is the answer of $x + 3y = 6$ and $2x + 3y = 12$.
Note: While solving the question, we can verify our answer by putting x and y coordinates in both the equation, and if coordinates satisfy both the equation then our answer is correct otherwise we have to find the answer again. Some points to be kept in mind while plotting lines are to use values of x = 0, 1, -1, 2, -2 instead of using bigger numbers to find corresponding values of y for plotting the graph; if at any point value of y comes out as a fraction, try to look for different values of x such that plotting becomes easier.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




