Question

How do we solve the equation \[a\sin x + b\cos x = c\] ?

Answer 1

Hint:We use trigonometric identities and trigonometric ratios to solve this problem. We will also learn some properties of trigonometry. We will use some concepts and formulae from general solutions of trigonometric equations, and hence solve this problem.

Complete step by step solution:
Here, solving this equation means finding the value of, which satisfies this equation.
In trigonometry, there is no unique solution but rather we have a principal solution. Generally, the principal solution lies in the range \[\left[ { - \pi ,\pi } \right]\] and all other solutions are called general solutions.
We will get a solution which is a combination of both general solution and principal solution.
The given equation is \[a\sin x + b\cos x = c\]
Now, divide the whole equation by \[\sqrt {{a^2} + {b^2}} \]
\[ \Rightarrow \dfrac{a}{{\sqrt {{a^2} + {b^2}} }}\sin x + \dfrac{b}{{\sqrt {{a^2} + {b^2}} }}\cos x = \dfrac{c}{{\sqrt {{a^2} + {b^2}} }}\] ------(1)
Now, consider this triangle

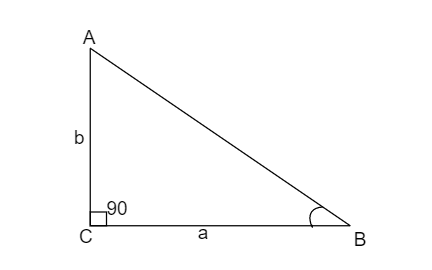
This is \[\vartriangle ABC\] , which is right-angled at angle “C”. And side \[BC\] is equal to “a” and side \[AC\] is equal to “b”.
Here, according to Pythagoras theorem, \[A{C^2} + B{C^2} = A{B^2}\]
\[ \Rightarrow A{B^2} = {a^2} + {b^2}\]
\[ \Rightarrow AB = \sqrt {{a^2} + {b^2}} \]
Now, applying trigonometric ratios, we get,
 \[\sin B = \dfrac{{AC}}{{AB}} = \dfrac{b}{{\sqrt {{a^2} + {b^2}} }}\] and \[\cos B = \dfrac{{BC}}{{AB}} = \dfrac{a}{{\sqrt {{a^2} + {b^2}} }}\]
Now consider \[\angle B = \alpha \]
So, \[\sin \alpha = \dfrac{b}{{\sqrt {{a^2} + {b^2}} }}\] and \[\cos \alpha = \dfrac{a}{{\sqrt {{a^2} + {b^2}} }}\] -----(2)
Substitute these values in equation (1)
\[ \Rightarrow \cos \alpha \sin x + \sin \alpha \cos x = \dfrac{c}{{\sqrt {{a^2} + {b^2}} }}\]
We know the identity that, \[\cos B\sin A + \sin B\cos A = \sin (A + B)\]
So, we get,
\[ \Rightarrow \sin (x + \alpha ) = \dfrac{c}{{\sqrt {{a^2} + {b^2}} }}\]
And according to general solutions concept,
The general solution of equation \[\sin \theta = k\] is \[n\pi + {\left( { - 1} \right)^n}\phi ,n \in Z\] where \[\phi \] is the principal solution.
The general solution of equation \[\cos \theta = k\] is \[2n\pi \pm \phi ,n \in Z\] where \[\phi \] is the principal solution.
The general solution of equation \[\tan \theta = k\] is \[n\pi + \phi ,n \in Z\] where \[\phi \] is the principal solution.
So, according to this,
\[ \Rightarrow \sin (x + \alpha ) = \dfrac{c}{{\sqrt {{a^2} + {b^2}} }}\]
\[ \Rightarrow x + \alpha = n\pi + {( - 1)^n}{\sin ^{ - 1}}\left( {\dfrac{c}{{\sqrt {{a^2} + {b^2}} }}} \right)\]
Transposing \[\alpha \] to other side,
\[ \Rightarrow x = n\pi + {( - 1)^n}{\sin ^{ - 1}}\left( {\dfrac{c}{{\sqrt {{a^2} + {b^2}} }}} \right) - \alpha \] ----where \[n \in Z\] .
We can substitute, \[\alpha = {\sin ^{ - 1}}\left( {\dfrac{b}{{\sqrt {{a^2} + {b^2}} }}} \right)\] or \[\alpha = {\cos ^{ - 1}}\left( {\dfrac{a}{{\sqrt {{a^2} + {b^2}} }}} \right)\] from equation (2)
So, this is the solution of the given equation.

Note:
In this problem, we considered \[\sin B\] and \[\cos B\] values. But instead, we can also consider \[\sin A = \dfrac{a}{{\sqrt {{a^2} + {b^2}} }}\] and \[\cos A = \dfrac{b}{{\sqrt {{a^2} + {b^2}} }}\]
And upon taking \[\angle A = \beta \] , we get, \[\sin \beta \sin x + \cos \beta \cos x = \dfrac{c}{{\sqrt {{a^2} + {b^2}} }}\]
\[ \Rightarrow \cos (x - \beta ) = \dfrac{c}{{\sqrt {{a^2} + {b^2}} }}\]
And from general solution concepts, we get,
\[ \Rightarrow x - \beta = 2n\pi \pm {\cos ^{ - 1}}\left( {\dfrac{c}{{\sqrt {{a^2} + {b^2}} }}} \right)\]
\[ \Rightarrow x = 2n\pi \pm {\cos ^{ - 1}}\left( {\dfrac{c}{{\sqrt {{a^2} + {b^2}} }}} \right) + \beta \]
So, this is also a solution for the given equation.