Question

Solve system of equation x+y+xy=11 and ${{\text{x}}^2}{\text{y}} + {\text{x}}{{\text{y}}^2} = 30$\[\]

Answer 1

Hint-Proceed the solution of this question by visualising some rearrangements so that values of some terms can be replaced from one equation into other equations so quadratic can be formed. If once quadratic gets formed, then we can reach the desired solution pairs.
Complete step-by-step answer:
In the question, it is given two system of equation as
⇒x+xy+y=11……………. (i)
⇒${{\text{x}}^2}{\text{y}} + {\text{x}}{{\text{y}}^2} = 30$ …………………(ii)
Taking xy common from equation (ii)
⇒xy(x+y) =30 …………… (iii)
Equation (i) can be written as
⇒xy= 11-(x+y) …………. (iv)
put value of xy in (iii)
⇒ [11-(x+y)] (x+y) =30
let x+y= z
therefore, (11-z) z=30
On opening the bracket
therefore, $11{\text{z - }}{{\text{z}}^2} = 30$
this can be written as
⇒${{\text{z}}^2} - 11z + 30 = 0$
We have, a quadratic equation ${{\text{z}}^2} - 11z + 30 = 0$
Sridharacharya formula is actually the quadratic formula, used for finding the roots of a quadratic equation \[{\text{a}}{{\text{x}}^2}{\text{ + bx + c = 0}}\] , where a not equal to 0 , & a, b, c are real coefficients of the equation \[{\text{a}}{{\text{x}}^2}{\text{ + bx + c = 0}}\]
Being quadratic it has 2 roots.
⇒X = $\dfrac{{\left( { - {\text{b + }}\sqrt {{{\text{b}}^2} - 4{\text{ac}}} } \right)}}{{2{\text{a}}}}{\text{ & }}\dfrac{{\left( { - {\text{b - }}\sqrt {{{\text{b}}^2} - 4{\text{ac}}} } \right)}}{{2{\text{a}}}}$ (1)

On comparing the given equation ${{\text{z}}^2} - 11z + 30 = 0$ with the general quadratic equation \[{\text{a}}{{\text{x}}^2}{\text{ + bx + c = 0}}\] we got values of coefficients a = 1, b = -11, c = 30
On putting the value of coefficients a, b, c in equation (1)
⇒${\text{z = }}\dfrac{{\left( { - ( - 11){\text{ + }}\sqrt {{{( - 11)}^2} - 4 \times (1) \times (30)} } \right)}}{{2 \times 1}}{\text{ & }}\dfrac{{\left( { - ( - 11){\text{ - }}\sqrt {{{( - 11)}^2} - 4 \times (1) \times (30)} } \right)}}{{2 \times 1}}$
⇒${\text{z = }}\dfrac{{\left( {{\text{11 + }}\sqrt 1 } \right)}}{2}{\text{ & }}\dfrac{{\left( {{\text{11 - }}\sqrt 1 } \right)}}{2}$
⇒${\text{z = }}\dfrac{{\left( {{\text{11 + 1}}} \right)}}{2}{\text{ & }}\dfrac{{\left( {{\text{11 - }}1} \right)}}{2}$
⇒${\text{z = 6 \& 5}}$
We know that if discriminant D $ \geqslant {\text{0}}$ then it will give real and distinct roots.
Here D= ${\text{ = }}\sqrt {{{( - 11)}^2} - 4 \times 1 \times (30)} {\text{ = }}\sqrt 1 {\text{ }} \geqslant {\text{0}}$ Therefore we got two distinct real roots
⇒${{\text{z}}_1}{\text{ = 6 \& }}{{\text{z}}_2}{\text{ = 5}}$
we got z=5 or z=6
therefore, x+y can be equal to 5 or 6) [$\because $ x+y= z]
as 11-(x+y) =xy
therefore, we will take cases
case 1
when x+y=5 then, xy=6.
By hit and trial method
The only two cases thus formed are {2,3} and {3,2}
Here we cannot take individually x or y = 6 because in equation (ii) it is clearly given that ${{\text{x}}^2}{\text{y}} + {\text{x}}{{\text{y}}^2} = 30$. if x is 6 then {${{\text{x}}^2}{\text{y}} + {\text{x}}{{\text{y}}^2} = 30$} is greater than 30 which is not possible.
case 2
when x+y=6
then, xy=5
By hit and trial method
The only cases formed are {5,1} and {1,5}
so the final answer would be {1,5}; {5,1}; {2,3} and {3,2}.

Note- This type of particular question, we can also solve by drawing the graph and intersection point will give our possible values of x and y pairs. Yes, given the system of equations in question are not any standard function but by hit and trial and arbitrary taking some points and on plotting them with proper scale, we can locate intersection points which are our desired values of x and y.
As shown in the given graph, in the 1st quadrant, both functions come to close so it seems like they are coinciding. But in figure 2 it shows that they are not coinciding their values are getting differ after 2 places of decimal
 

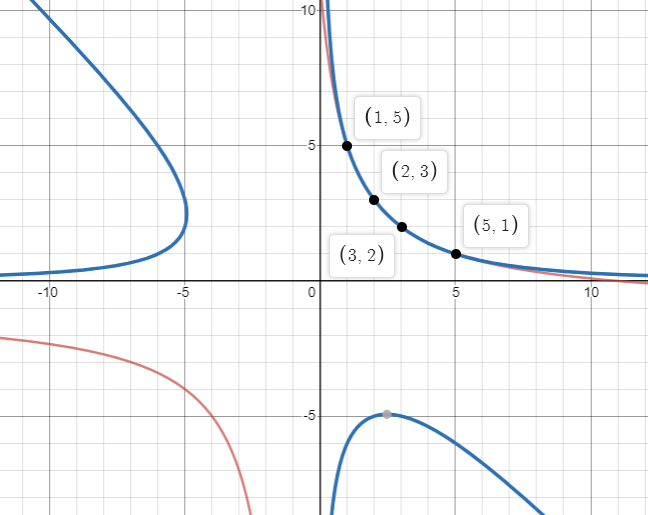
                                                                     fig (1)

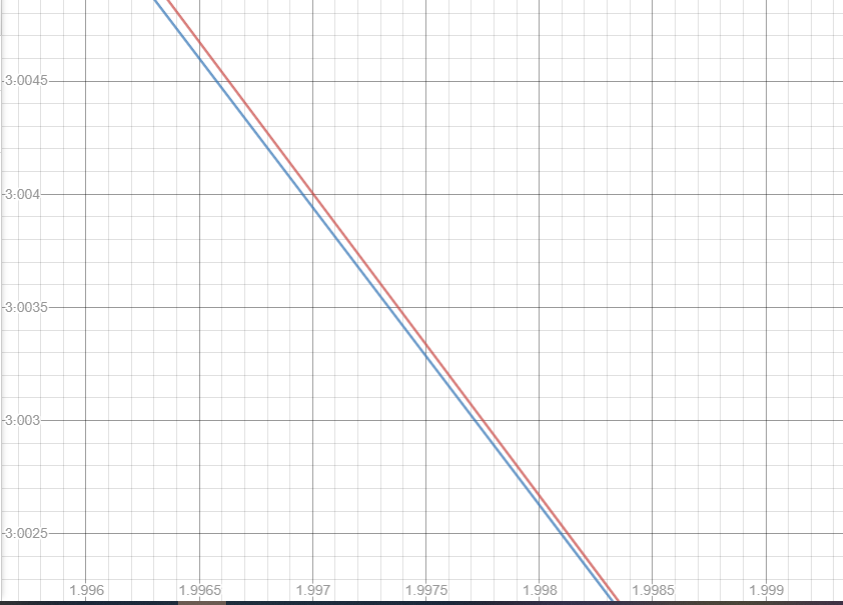
                                                                            fig (2)