Question

Solve: \[\sin \left( {{\tan }^{-1}}x \right),\left| x \right|<1\] is equal to
A. \[\dfrac{x}{\sqrt{1-{{x}^{2}}}}\]
B. \[\dfrac{1}{\sqrt{1-{{x}^{2}}}}\]
C. \[\dfrac{1}{\sqrt{1+{{x}^{2}}}}\]
D. \[\dfrac{x}{\sqrt{1+{{x}^{2}}}}\]

Answer 1

Hint: To solve the question, we need to assume that the value of \[{{\tan }^{-1}}x\] is \[\text{ }\!\!\theta\!\!\text{ }\] and then place the value in place of \[{{\tan }^{-1}}x\] to find the value of \[\sin \text{ }\!\!\theta\!\!\text{ }\] and remove \[\text{ }\!\!\theta\!\!\text{ }\] by the trigonometric value of \[{{\tan }^{-1}}x\] . The formula for \[\tan \text{ }\!\!\theta\!\!\text{ }\] is
 \[\tan \text{ }\!\!\theta\!\!\text{ }=\dfrac{\text{height}}{\text{base}}\] of an assumed triangle and then find the value of \[\text{ }\!\!\theta\!\!\text{ }\] and place it with \[\sin \text{ }\!\!\theta\!\!\text{ }\] to find the value of \[\sin \text{ }\!\!\theta\!\!\text{ }\] in terms of \[x\] .

Complete step-by-step answer:
Let us first draw a triangle based on the question with \[\text{ }\!\!\theta\!\!\text{ }\] as angle at point A.

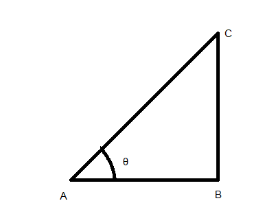
where \[{{\tan }^{-1}}x\] which means if we equate the value of \[x\] in terms of \[\text{ }\!\!\theta\!\!\text{ }\] , we get the value of \[x\] as:
 \[\Rightarrow {{\tan }^{-1}}x=\text{ }\!\!\theta\!\!\text{ }\]
 \[\Rightarrow x=\tan \text{ }\!\!\theta\!\!\text{ }\]
Now according to the trigonometric formula, the value of the \[\text{tangent}\] is given as:
 \[\tan \text{ }\!\!\theta\!\!\text{ }=\dfrac{\text{height}}{\text{base}}\]
Equating the value of \[\tan \text{ }\!\!\theta\!\!\text{ }=x\] with \[\tan \text{ }\!\!\theta\!\!\text{ }=\dfrac{\text{height}}{\text{base}}\] , we get the value of the ratio of \[\dfrac{\text{height}}{\text{base}}\] as \[\dfrac{x}{1}\] .
Therefore, we can say that the height of the triangle is \[x\] and the base is \[1\] . Using Pythagoras theorem we can find the value of the hypotenuse of the triangle as:
Hypotenuse \[=\sqrt{\text{heigh}{{\text{t}}^{2}}+\text{bas}{{\text{e}}^{2}}}\]
 \[\Rightarrow \sqrt{{{x}^{2}}+{{\text{1}}^{2}}}\]
Now as we have all the values i.e. height, base and hypotenuse we can find the value of \[\sin \left( {{\tan }^{-1}}x \right)\] by replacing it with \[\sin \text{ }\!\!\theta\!\!\text{ }\] and after that we find the value of \[\sin \text{ }\!\!\theta\!\!\text{ }\] as:
 \[\sin \text{ }\!\!\theta\!\!\text{ }=\dfrac{\text{height}}{\text{hypotenuse}}\]
Placing the values of height and hypotenuse in the above formula, we get the value of \[\sin \text{ }\!\!\theta\!\!\text{ }\] as:
 \[\Rightarrow \sin \text{ }\!\!\theta\!\!\text{ }=\dfrac{x}{\sqrt{{{x}^{2}}+1}}\]
Now on the L.H.S, the value of \[\sin \text{ }\!\!\theta\!\!\text{ }\] can be replaced by \[\sin \left( {{\tan }^{-1}}x \right)\] with \[{{\tan }^{-1}}x=\text{ }\!\!\theta\!\!\text{ }\] . Hence, the value of \[\sin \left( {{\tan }^{-1}}x \right)\] is \[\dfrac{x}{\sqrt{{{x}^{2}}+1}}\] .
So, the correct answer is “ \[\dfrac{x}{\sqrt{{{x}^{2}}+1}}\] ”.

Note: Student may make mistake as the value of inverse is such as \[{{\tan }^{-1}}x=\dfrac{1}{\tan x}\] , but \[{{\left( \tan x \right)}^{-1}}=\dfrac{1}{\tan x}\] . Hence such mistakes should be avoided and the angle should be taken in any one point of the triangle like A for both \[\tan \text{ }\!\!\theta\!\!\text{ }\] and \[\sin \text{ }\!\!\theta\!\!\text{ }\] .