Question

How do you solve ${\sin ^2}x - 5\cos x = 5$ and find all solutions in the interval $\left[ {0,2\pi } \right)$?

Answer 1

Hint: irst, move $5$ to the left side of the equation. Then, replace ${\sin ^2}x$ with $1 - {\cos ^2}x$ and factor it by grouping. Set the first and second factor equal to $0$ and solve using trigonometric properties. Next, find all values of $x$ in the interval $\left[ {0,2\pi } \right)$. Then, we will get all the solutions of the given equation in the given interval.

Complete step by step solution:
Given equation: ${\sin ^2}x - 5\cos x = 5$
We have to find all possible values of $x$ in the interval $\left[ {0,2\pi } \right)$.
First, move $5$ to the left side of the equation.
${\sin ^2}x - 5\cos x - 5 = 0$
Replace ${\sin ^2}x$ with $1 - {\cos ^2}x$.
$1 - {\cos ^2}x - 5\cos x - 5 = 0$
Reorder terms.
$ - {\cos ^2}x - 5\cos x - 4 = 0$
It can be written as
${\cos ^2}x + 5\cos x + 4 = 0$
Now, factor by grouping.
For a polynomial of the form $a{x^2} + bx + c$, rewrite the middle term as a sum of two terms whose product is $a \times c = 1 \times 4 = 4$ and whose sum is $b = 5$.
Rewrite $5$ as $4$ plus $1$.
${\cos ^2}x + \left( {4 + 1} \right)\cos x + 4 = 0$
Apply the distributive property.
${\cos ^2}x + \cos x + 4\cos x + 4 = 0$
Factor out the greatest common factor from each group.
Group the first two terms and the last two terms.
$\left( {{{\cos }^2}x + \cos x} \right) + \left( {4\cos x + 4} \right) = 0$
Factor out the greatest common factor (GCF) from each group.
$\cos x\left( {\cos x + 1} \right) + 4\left( {\cos x + 1} \right) = 0$
Factor the polynomial by factoring out the greatest common factor, $\cos x + 1$.
$\left( {\cos x + 1} \right)\left( {\cos x + 4} \right) = 0$
If any individual factor on the left side of the equation is equal to $0$, the entire expression will be equal to $0$.
$\cos x + 1 = 0$
$\cos x + 4 = 0$
Set the first factor equal to $0$ and solve.
$\cos x + 1 = 0$
Subtract $1$ from both sides of the equation.
$\cos x = - 1$…(i)
Now, using the property $\cos \left( {\pi - x} \right) = - \cos x$ and $\cos 0 = 1$ in equation (i).
$ \Rightarrow \cos x = - \cos 0$
$ \Rightarrow \cos x = \cos \left( {\pi - 0} \right)$
$ \Rightarrow x = \pi $
Since, the period of the $\cos x$ function is $2\pi $ so values will repeat every $2\pi $ radians in both directions.
$x = \pi + 2n\pi $, for any integer $n$.
Now, set second factor equal to $0$ and solve.
$\cos x + 4 = 0$
Subtract $4$ from both sides of the equation.
$\cos x = - 4$
The range of cosine is $ - 1 \leqslant y \leqslant 1$. Since $ - 4$ does not fall in this range, there is no solution.
No solution
Thus, $x = \pi + 2n\pi $
Where, $n$ is any integer, i.e., $n = 0, \pm 1, \pm 2, \pm 3,......$
Now, find all values of $x$ in the interval $\left[ {0,2\pi } \right)$.
Since, it is given that $x \in \left[ {0,2\pi } \right)$, hence put $n = 0$ in the general solution.
So, putting $n = 0$ in the general solution, $x = \pi + 2n\pi $, we get
$x = \pi $

Hence, $x = \pi $ is the only solution of the given equation in the given interval.

Note: In above question, we can find the solutions of given equation by plotting the equation, ${\sin ^2}x - 5\cos x = 5$ on graph paper and determine all solutions which lie in the interval, $\left[ {0,2\pi } \right)$.
 

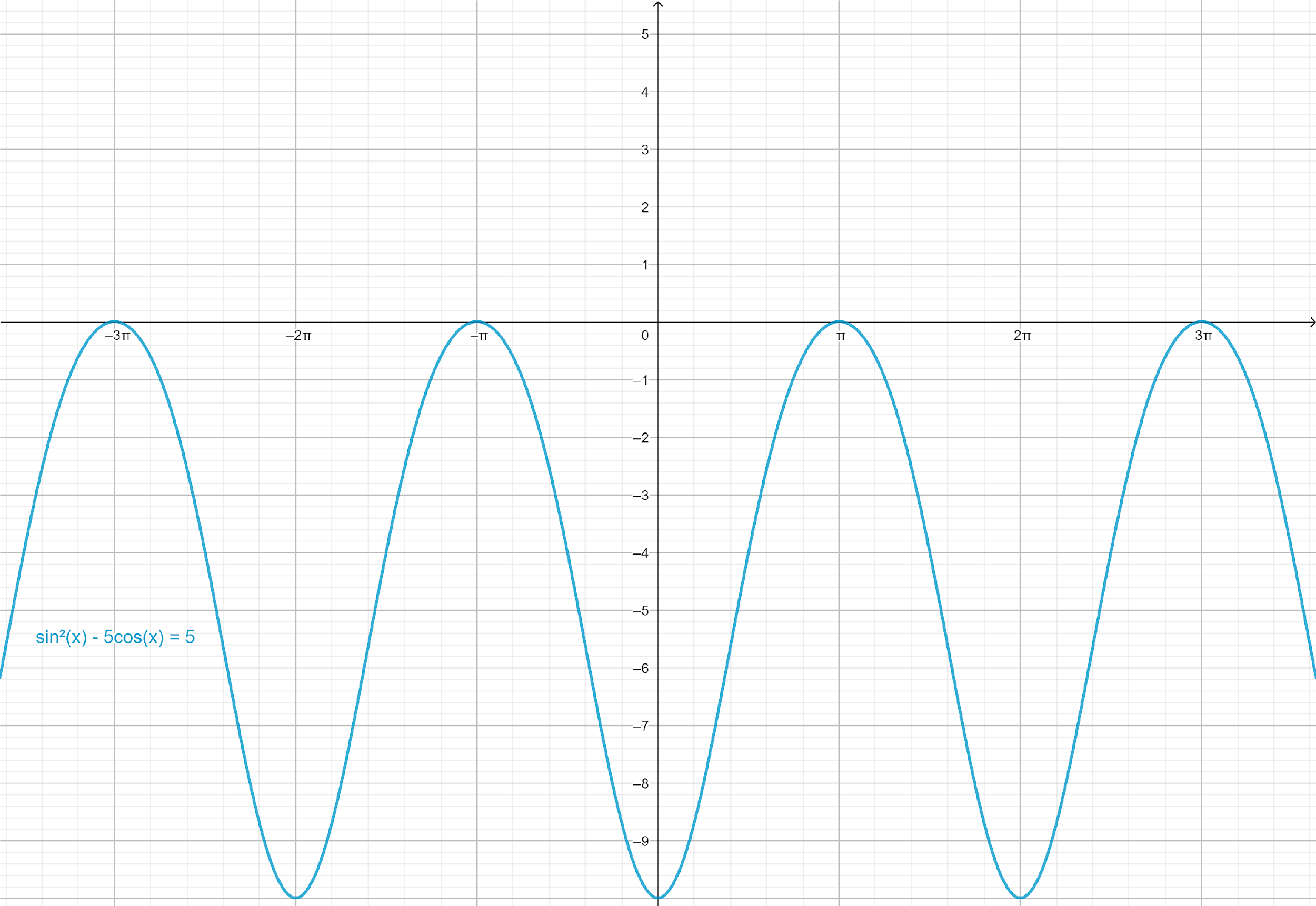
From the graph paper, we can see that there is only one value of $x$ in the interval $\left[ {0,2\pi } \right)$.