Question

How do you solve “ quotient of three times a number and 4 is at least -16” and graph the solution on a number line?.

Answer 1

Hint: In order to determine the solution and graph of the statement , first we have to obtain a mathematical expression from the statement by assuming the unknown number in the statement as $ x $ and using the $ \left( \geqslant \right) $ equal to or greater than inequality symbol to frame the inequality as $ \dfrac{{3x}}{4} \geqslant - 16 $ .To the obtain the solution , multiply both sides with the $ \dfrac{4}{3} $ .Graph the solution with the solid line vertical to the point $ - \dfrac{{64}}{3} $ on the horizontal axis.

Complete step-by-step answer:
In order to solve the question, I have to first obtain a mathematical expression from the statement given in the question.
In order to write any mathematical expression from some words and figures, we must first find the relationship and the quantities specified And later turn these words into expression
Let’s look into our question what written in it “How many fourths in 3 fourths”
Let’s break our question into two parts i.e. “quotient of three times a number and 4 is at least -16 “
“number” in the statement is some unknown value, so let it be called $ x $ .
As we know quotients consist of a numerator and denominator and in our case the numerator is $ 3x $ and the denominator is $ 4 $ and this quotient is at least -16 or in other words we can say it is equal to or greater than -16 .
To represent the equal to or greater than relationship we use the $ \geqslant $ inequality symbol.
Lets just combine all these things, we get inequality
 $ \dfrac{{3x}}{4} \geqslant - 16 $ ---(1)
Hence, we have successfully framed our expression. Now we have to solve it for variable $ x $
Multiplying both sides of the inequality (1)with the number $ \dfrac{4}{3} $ , we get
 $ \dfrac{4}{3}\left( {\dfrac{{3x}}{4}} \right) \geqslant \left( { - 16} \right)\left( {\dfrac{4}{3}} \right) $
Simplifying it further, we get
 $ x \geqslant - \dfrac{{64}}{3} $
Or in the set form $ \left[ { - \dfrac{{64}}{3},\infty } \right) $
To graph the solution $ x \geqslant - \dfrac{{64}}{3} $ , draw a solid line parallel to y-axis at $ - \dfrac{{64}}{3} $ on the horizontal axis.
The line is the solid line as the inequality contains the “or equal to “condition .
Shade the right-hand side part of the line as the inequality contains the “greater than” condition for the variable $ x $ .
Graph of the solution $ x \geqslant - \dfrac{{64}}{3} $ is as shown below:

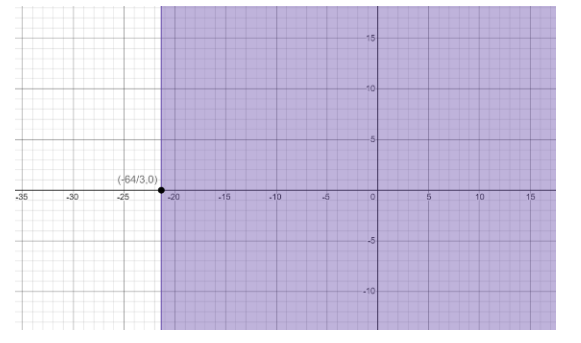
Therefore, we have successfully obtained the graph of the solution $ x \geqslant - \dfrac{{64}}{3} $

Note: Linear Inequality: A linear equality is a mathematical expression in which two values or two expressions are compared with each other. They are compared with the inequality symbols like $ < , > , \geqslant , \leqslant $ .Values can be either numerical / algebraic or can be a combination of both . The inequality symbols ( $ < , > $ )are used to express strict inequalities and on the other hand symbols $ ( \geqslant , \leqslant ) $ are slack inequalities