Question

How do you solve \[\ln (x - 6) - \ln (5) = \ln (7) + \ln (x - 2)\] ?

Answer 1

Hint: In order to simplify the natural log equation with the formula is \[\ln (x \cdot z) = \ln x + \ln z\] and \[\ln \dfrac{x}{z} = \ln x - \ln z\] .The natural logarithm of a number is its logarithm to the base of the mathematical constant. The natural logarithm of \[x\] is generally written as \[\ln x,{\log _e}x\] or sometimes, if the base \[e\] is implicit, simply \[\log x\] . We get the required solution by comparing the formula.
Formula:
 \[\ln (x \cdot z) = \ln x + \ln z\]
 \[\ln \dfrac{x}{z} = \ln x - \ln z\] .

Complete step-by-step answer:
In this problem,
The natural logarithm of the equation is \[\ln (x - 6) - \ln (5) = \ln (7) + \ln (x - 2)\] . First, we compare the equation with the formula is \[\ln (x \cdot z) = \ln x + \ln z\] and \[\ln \dfrac{x}{z} = \ln x - \ln z\] .
LHS \[ = \] RHS
 \[\ln (x - 6) - \ln (5) = \ln (7) + \ln (x - 2)\]
Comparing LHS equation, \[\ln (x - 6) - \ln (5)\] with the formula \[\ln \dfrac{x}{z} = \ln x - \ln z\] , Subtraction of the log is the result of the source values being divided, where \[x = (x - 6),z = 5\]
LHS: \[\ln (x - 6) - \ln (5) = \ln \left( {\dfrac{{x - 6}}{5}} \right)\]
 and Comparing RHS equation, \[\ln (7) + \ln (x - 2)\] with the formula \[\ln (x \cdot z) = \ln x + \ln z\] ,Addition of logs is the consequence of the source values being multiplied. So
RHS: \[\ln (7) + \ln (x - 2) = \ln (7(x - 2))\] .
Combining all this equation together, we can get
 \[\ln \left( {\dfrac{{x - 6}}{5}} \right) = \ln (7(x - 2)\]
By remove the inverse of log on both side, we get
 \[\left( {\dfrac{{x - 6}}{5}} \right) = (7(x - 2)\]
Expanding the bracket on RHS and multiply by \[5\] on both sides, we have
 \[\
  x - 6 = 35(x - 2) \\
  x - 6 = 35x - 70 \;
\ \]
By simplify the equation to get the value of \[x\] , we get
 \[x - 35x = 6 - 70 \Rightarrow - 34x = - 54\]
 \[x = \dfrac{{54}}{{34}} = \dfrac{{27}}{{17}} = 1.588\]
Therefore the required solution, \[x = 1.588\] .
So, the correct answer is “\[x = 1.588\] ”.

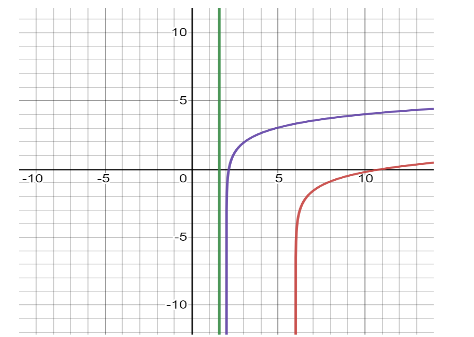
Note: First we have to plot a graph with respect to the problem is shown below.
The graph of the red curve represent the equation \[\ln (x - 6) - \ln (5)\]
The graph of the blue curve represent the equation \[\ln (x - 6) - \ln (5)\]
The graph of the green line is \[x = 1.588\]

In this problem, we have to remember the natural logarithm formula \[\ln (x \cdot z) = \ln x + \ln z\] and \[\ln \dfrac{x}{z} = \ln x - \ln z\] on comparing with the given equation to get the required value \[x\] .