Question

How to solve \[\ln \left( 1+x \right)=1+\ln x\]?

Answer 1

Hint: Convert 1 in the R.H.S. into logarithmic form by using the relation \[1=\ln e\]. Now, apply the formula: - \[\log m+\log n=\log \left( mn \right)\] in the R.H.S. to simplify. Remove the logarithmic function from both the sides and form a linear equation in x. Solve this equation to get the value of x. Check if this value is valid or not by using the fact that ‘argument of log function must be greater than 0’.

Complete step by step answer:
Here, we have been provided with the logarithmic equation: \[\ln \left( 1+x \right)=1+\ln x\]. We are asked to solve this equation, that means we have to find the value of x.
Now, here we have ln, i.e., natural log or log to the base e, so we can write 1 in the R.H.S. and \[\ln e\] or \[{{\log }_{e}}e\]. Therefore, the equation becomes: -
\[\Rightarrow \ln \left( 1+x \right)=\ln e+\ln x\]
Applying the sum to product rule of log given as: - \[\log m+\log n=\log \left( mn \right)\], we get in the R.H.S.,
\[\Rightarrow \ln \left( 1+x \right)=\ln \left( ex \right)\]
Now, comparing the arguments of log on both the sides by removing the logarithmic function, we get,
\[\Rightarrow 1+x=ex\]
Clearly, the above equation is a linear equation in x, so let us solve this equation for the value of x,
\[\Rightarrow ex-x=1\]
Taking x common in the L.H.S., we get,
\[\Rightarrow x\left( e-1 \right)=1\]
Dividing both the sides with (e – 1), we get,
\[\Rightarrow x=\left( \dfrac{1}{e-1} \right)\]
Now, let us check if this value of $x$ obtained is valid or not. We know that the logarithmic function is defined when its argument and base is greater than $0$ and also base is unequal to 1. Here, we have log to the base e is nearly $2.71$ which is greater than 0 and also unequal to 1. So, the base is defined. Now, let us define the argument. We have $(x + 1)$ and $x$ as the variable arguments, so we must have,
(i) \[x+1>0\Rightarrow x>-1\Rightarrow x\in \left( -1,\infty \right)\]
(ii) \[x>0\Rightarrow x\in \left( 0,\infty \right)\]
Since, we need to satisfy both the conditions, therefore we must consider the intersection of the two sets of values of x obtained. So, we have,

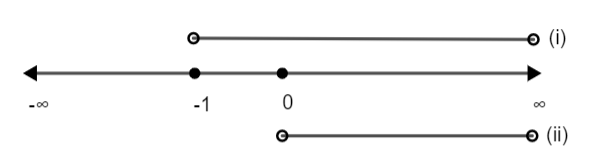
Therefore, \[x\in \left( 0,\infty \right)\] is the final condition.
Clearly, we can see that \[x=\dfrac{1}{e-1}\] is greater than 0.
Hence, \[x=\dfrac{1}{e-1}\] is our answer.

Note: One may note that we cannot remove the logarithmic function directly from the initial expression: - \[{{\log }_{e}}\left( 1+x \right)={{\log }_{e}}e+{{\log }_{e}}x\] as it will be a wrong approach. First, we need to convert the two logarithmic terms in the R.H.S. into a single logarithmic term by using the sum to product rule and then only we can compare the arguments. Remember that we must check the value of x obtained if it is valid or not by defining the argument and base of the log function.