Question

How do you solve \[\left( {x - 4} \right)\left( {x + 3} \right) < 0\]?

Answer 1

Hint: We have to find all possible values of $x$ satisfying given inequality. For this solve each inequation and obtain their solution sets. Also, represent them on a real line. Then, find the intersection of the solutions sets obtained by taking the help of the graphical representation of the solution sets. Thus, the set obtained is the required solution set of the given system of inequations.

Complete step by step solution:
Given: \[\left( {x - 4} \right)\left( {x + 3} \right) < 0\]
We have to find all possible values of $x$ satisfying given inequality.
Since, the product of two factors is negative.
So, one factor will be less than 0 and other will be greater than 0.
Thus, $x + 3 < 0,x - 4 > 0$ or $x + 3 > 0,x - 4 < 0$.
The system of inequalities is
$x + 3 < 0$…(i)
$x - 4 > 0$…(ii)
So, first we will solve inequation (i).
Collect all terms involving the variable on one side of the inequation and the constant terms on the other side and simplify both sides of inequality in their simplest forms to reduce the inequation in the form $ax < b$.
For this, subtract $3$ to both sides of inequation (i).
So, by rule 1, $x < - 3$
Hence, any real number less than $ - 3$ is a solution of inequation (i).
These solutions can be graphed on real line as shown below:

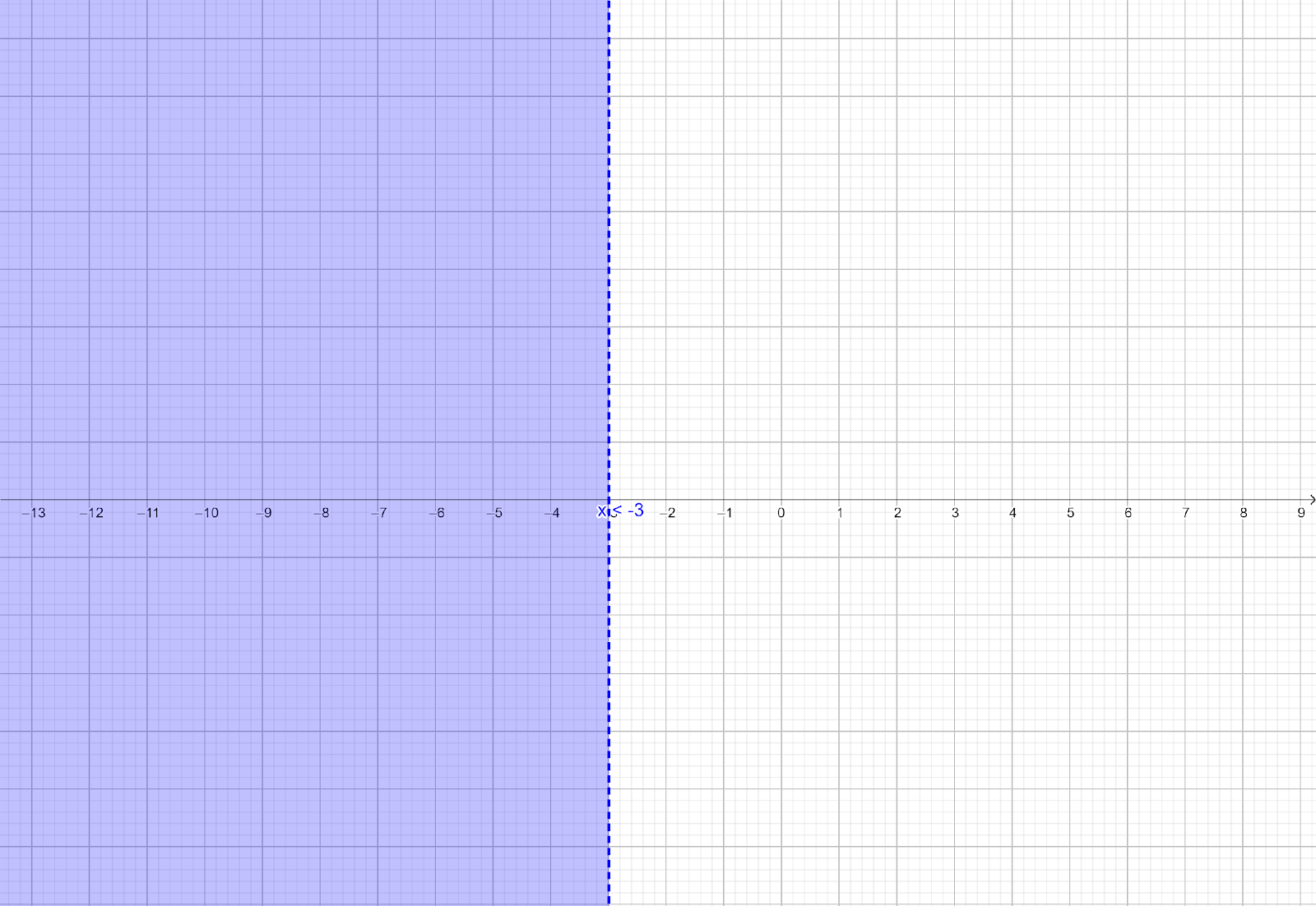The solution set of inequation (i) is $\left( { - \infty , - 3} \right)$.
Now, we will solve inequation (ii).
Collect all terms involving the variable on one side of the inequation and the constant terms on the other side and simplify both sides of inequality in their simplest forms to reduce the inequation in the form $ax > b$.
For this, add $4$ to both sides of inequation (ii).
So, by rule 1, $x > 4$
Hence, any real number greater than $4$ is a solution of inequation (ii).
These solutions can be graphed on real line as shown below:

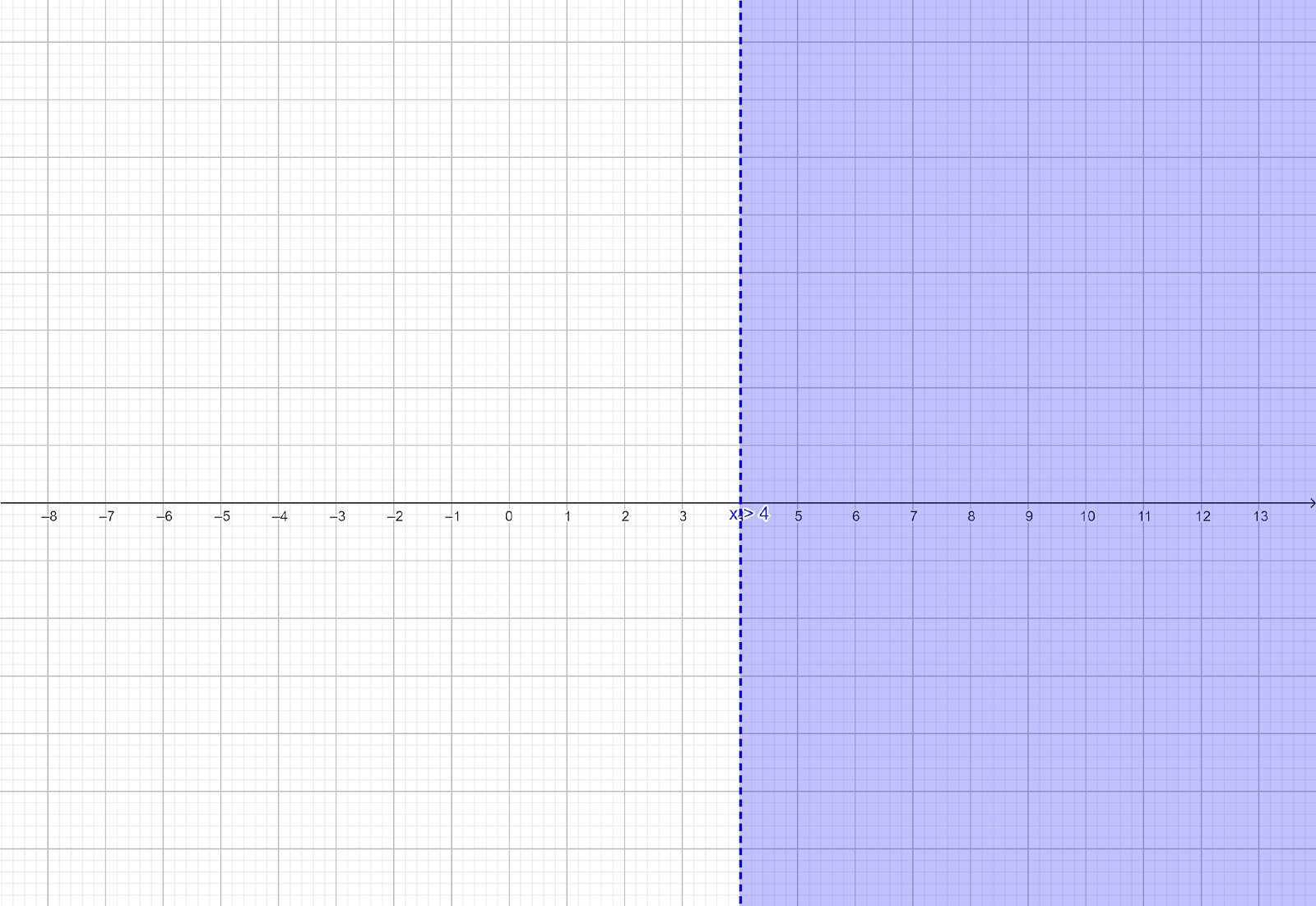The solution set of inequation (ii) is $\left( {4,\infty } \right)$.
We observe that there is no common solution of the two inequations.
The system of inequations is
$x + 3 > 0$…(iii)
$x - 4 < 0$…(iv)
So, first we will solve inequation (iii).
Collect all terms involving the variable on one side of the inequation and the constant terms on the other side and simplify both sides of inequality in their simplest forms to reduce the inequation in the form $ax > b$.
For this, subtract $3$ to both sides of inequation (iii).
So, by rule 1, $x > - 3$
Hence, any real number greater than $ - 3$ is a solution of inequation (iii).
These solutions can be graphed on real line as shown below:

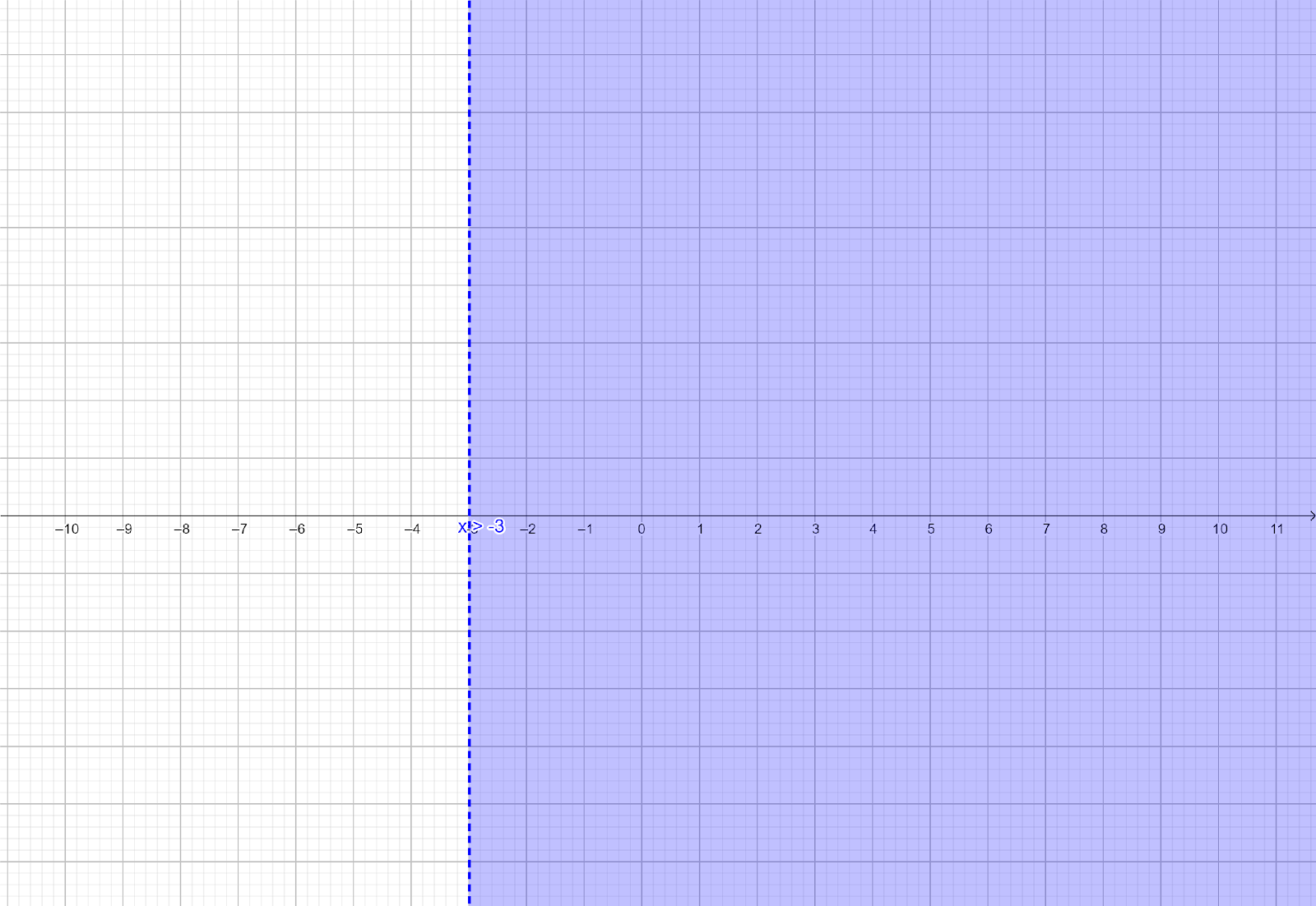The solution set of inequation (iii) is $\left( { - 3, + \infty } \right)$.
Now, we will solve inequation (iv).
Collect all terms involving the variable on one side of the inequation and the constant terms on the other side and simplify both sides of inequality in their simplest forms to reduce the inequation in the form $ax < b$.
For this, add $4$ to both sides of inequation (iv).
So, by rule 1, $x < 4$
Hence, any real number less than $4$ is a solution of inequation (iv).
These solutions can be graphed on real line as shown below:

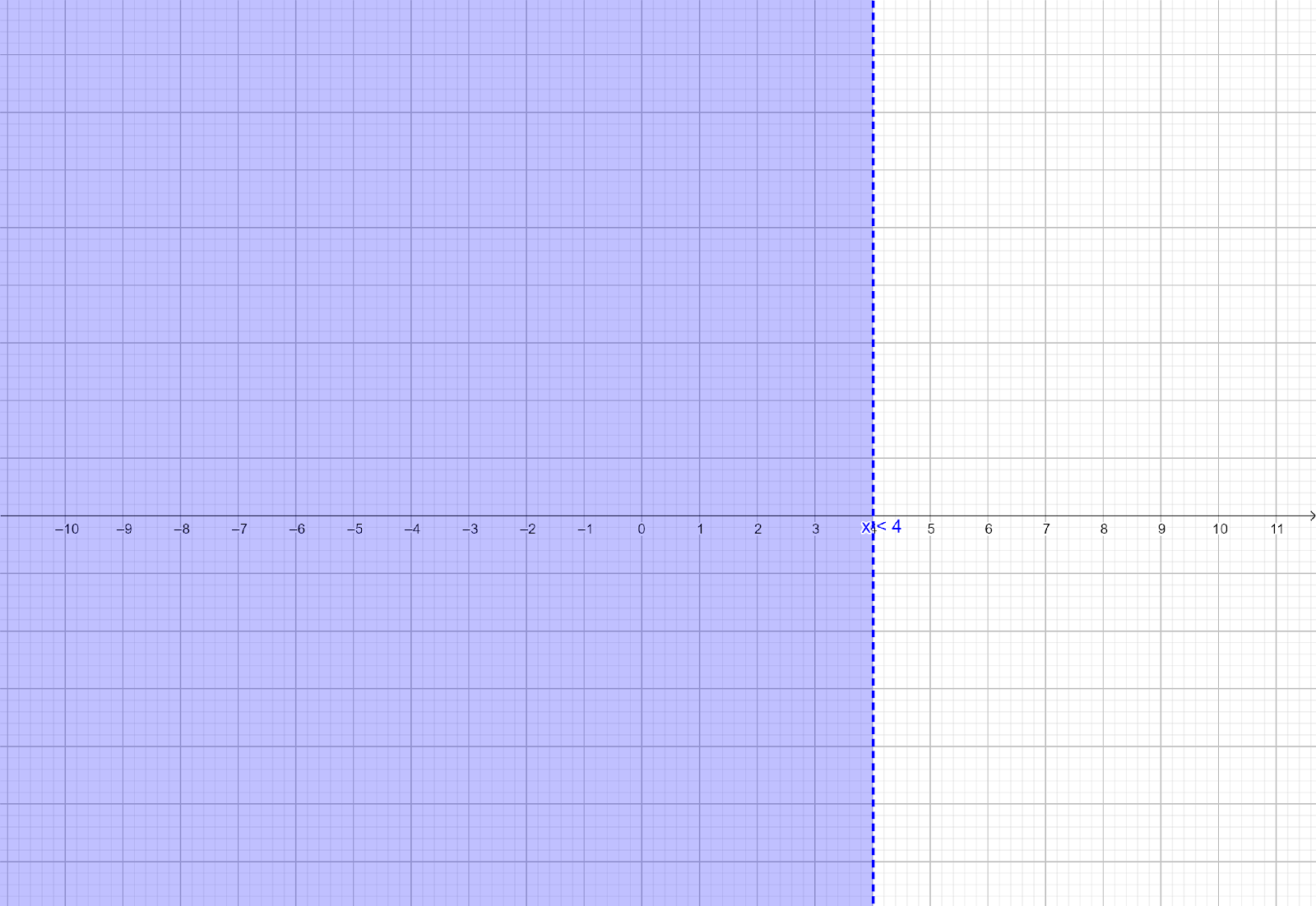The solution set of inequation (iv) is $\left( { - \infty ,4} \right)$.
We observe that $\left( { - 3,4} \right)$ is a common solution of the two inequalities.

Thus, $\left( { - 3,4} \right)$ is the required solution set of the given inequation.

Note: In order to solve a system of linear inequalities in one variable, we follow the following algorithm.
Algorithm:
Step I Obtain the system of linear inequations.
Step II Solve each inequation and obtain their solution sets. Also, represent them on a real line.
Step III Find the intersection of the solution sets obtained in step II by taking the help of the graphical representation of the solution sets in step II.
Step IV The set obtained in step III is the required solution set of the given system of inequations.