Question

How do you solve $\left| {5x + 11} \right| = 6$?

Answer 1

Hint: Here, we have to solve an absolute value equality which contains one absolute value. First, isolate the absolute value on one side of the equation. Next, check whether the number on the other side of the equation is negative. If our answer is yes, then the equation has no solution. If our answer is no, then go on to the next step. Next, write two equations without absolute values. The first equation will set the quantity inside the bars equal to the number on the other side of the equal sign; the second equation will set the quantity inside the bars equal to the opposite of the number on the other side. Next, solve the two equations and find the values of $x$.

Complete step by step answer:
Given equation: $\left| {5x + 11} \right| = 6$
We have to find all possible values of $x$ satisfying a given equation.
First, isolate the absolute value on one side of the equation.
Here, absolute value is already on the left-hand side of the equation.
Next, check whether the number on the other side of the equation is negative. If our answer is yes, then the equation has no solution. If our answer is no, then go on to the next step.
Here, $RHS = 6$, which is positive.
So, write two equations without absolute values. The first equation will set the quantity inside the bars equal to the number on the other side of the equal sign; the second equation will set the quantity inside the bars equal to the opposite of the number on the other side.
$5x + 11 = 6$…(1)
$5x + 11 = - 6$…(2)
Now, solve the two equations.
Subtract $11$ from both sides of equation (1) and (2).
$5x = - 5$ and $5x = - 17$
Now, divide both sides of the equation by $5$, we get
$x = - 1$ and $x = - \dfrac{{17}}{5}$
Final solution: Therefore, $x = - 1$ and $x = - \dfrac{{17}}{5}$ are solution of $\left| {5x + 11} \right| = 6$.

Note:
We can also determine the solution of $\left| {5x + 11} \right| = 6$ by graphing the given equation.
Graph of $\left| {5x + 11} \right| = 6$:

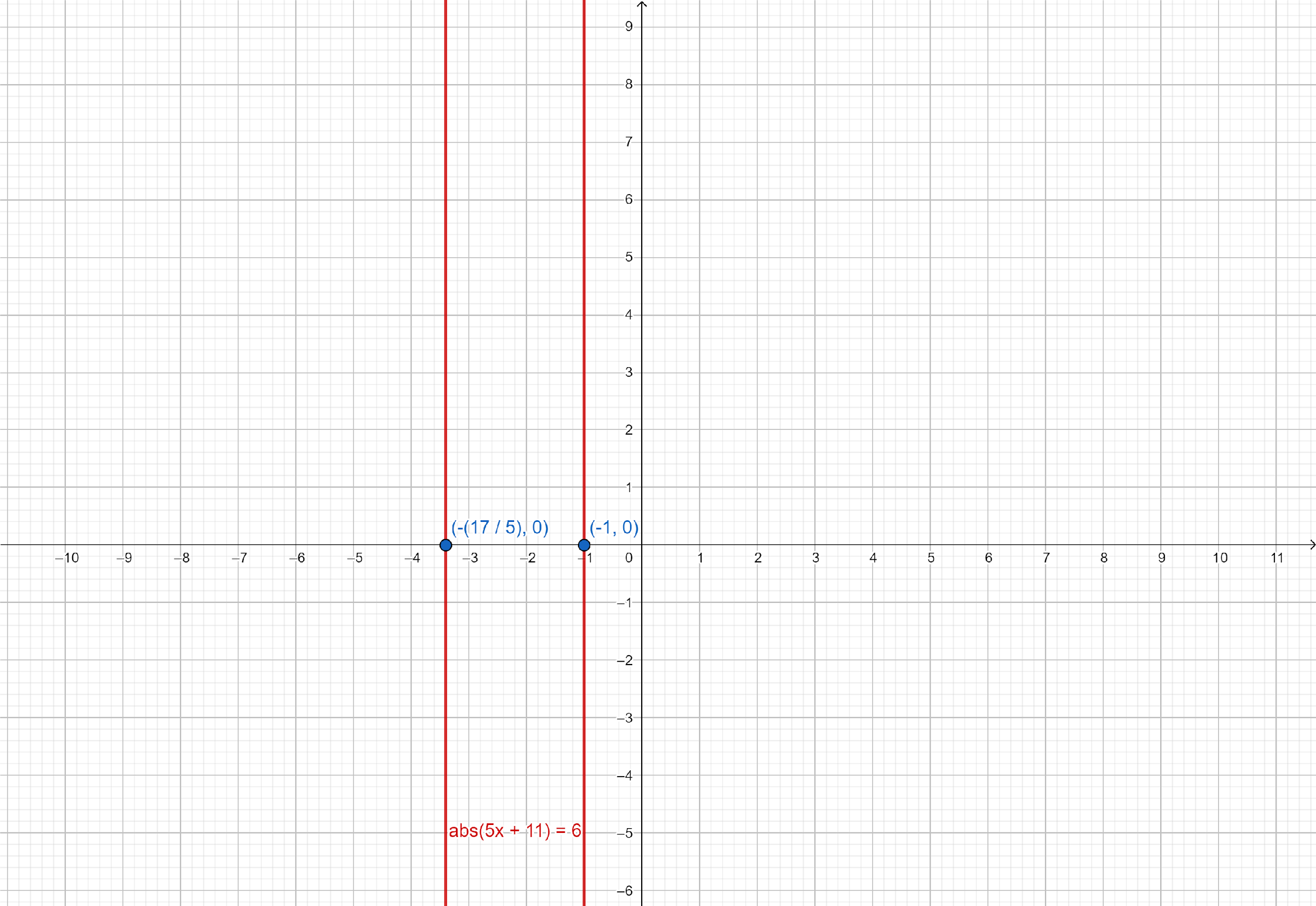
Final solution: Therefore, $x = - 1$ and $x = - \dfrac{{17}}{5}$ are solution of $\left| {5x + 11} \right| = 6$.