Question

How do you solve \[\left| {2x + 1} \right| < \left| {3x - 2} \right|\]?

Answer 1

Hint: We will divide both the sides by \[\left| {2x + 1} \right|\] then we know that \[\left| x \right| > a\] can also be written as \[ - a > x > a\]. Using this we will simplify it. Then taking the first and second term and then the second and third term we will find the interval of \[x\]. At last, we will combine to find the complete interval of solution of \[\left| {2x + 1} \right| < \left| {3x - 2} \right|\].

Complete step by step answer:
Given the inequality \[\left| {2x + 1} \right| < \left| {3x - 2} \right|\]
Since \[\left| {2x + 1} \right|\] is positive and we know that the inequality remains the same on dividing with a positive number. So, we get
\[ \Rightarrow \dfrac{{\left| {2x + 1} \right|}}{{\left| {2x + 1} \right|}} < \dfrac{{\left| {3x - 2} \right|}}{{\left| {2x + 1} \right|}}\]
Cancelling the common term and on rearranging, we get
\[ \Rightarrow \dfrac{{\left| {3x - 2} \right|}}{{\left| {2x + 1} \right|}} > 1\]
By the property we know that \[\dfrac{{\left| a \right|}}{{\left| b \right|}} = \left| {\dfrac{a}{b}} \right|\]. Using this, we get
\[ \Rightarrow \left| {\dfrac{{3x - 2}}{{2x + 1}}} \right| > 1\]
We know that \[\left| x \right| > a\] can also be written as \[ - a > x > a\]. Using this, we get
\[ \Rightarrow - 1 > \dfrac{{3x - 2}}{{2x + 1}} > 1\]
Now we solve first inequality: \[ - 1 > \dfrac{{3x - 2}}{{2x + 1}}\]
Adding \[1\] on both the sides of the equation and on rearranging, we get
\[ \Rightarrow \dfrac{{3x - 2}}{{2x + 1}} + 1 < 0\]
On taking the LCM, we get
\[ \Rightarrow \dfrac{{3x - 2 + 2x + 1}}{{2x + 1}} < 0\]
\[ \Rightarrow \dfrac{{5x - 1}}{{2x + 1}} < 0\]
Taking \[5\] common from the numerator and \[2\] common from the denominator, we get
\[ \Rightarrow \dfrac{5}{2}\dfrac{{\left( {x - \dfrac{1}{5}} \right)}}{{\left( {x + \dfrac{1}{2}} \right)}} < 0\]
Multiplying both the sides by \[\dfrac{2}{5}\], we get
\[ \Rightarrow \dfrac{{\left( {x - \dfrac{1}{5}} \right)}}{{\left( {x + \dfrac{1}{2}} \right)}} < 0\]
On solving, we get

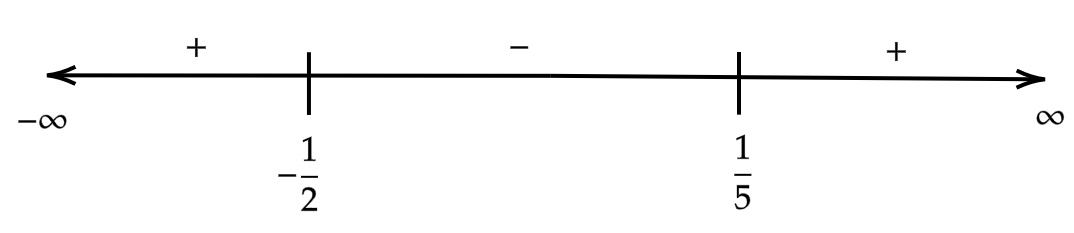
\[ \Rightarrow - \dfrac{1}{2} < x < \dfrac{1}{5} - - - (1)\]
This interval satisfies the linear inequality.
Now, consider \[\dfrac{{3x - 2}}{{2x + 1}} > 1\]
Subtracting \[1\] on both the sides of the equation, we get
\[ \Rightarrow \dfrac{{3x - 2}}{{2x + 1}} - 1 > 0\]
On taking the LCM, we get
\[ \Rightarrow \dfrac{{3x - 2 - 2x - 1}}{{2x + 1}} > 0\]
\[ \Rightarrow \dfrac{{x - 3}}{{2x + 1}} > 0\]
Taking \[2\] common from the denominator, we get
\[ \Rightarrow \dfrac{1}{2}\dfrac{{\left( {x - 3} \right)}}{{\left( {x + \dfrac{1}{2}} \right)}} > 0\]
Multiplying both the sides by \[2\], we get
\[ \Rightarrow \dfrac{{\left( {x - 3} \right)}}{{\left( {x + \dfrac{1}{2}} \right)}} > 0\]
On solving, we get

\[ \Rightarrow x < - \dfrac{1}{2}{\text{ and }}x > 3 - - - (2)\]
This interval satisfies the linear inequality.
So, from equation \[(1)\] and \[(2)\], we can write that \[x\] lies in the intervals \[\left( { - \infty , - \dfrac{1}{2}} \right) \cup \left( { - \dfrac{1}{2},\dfrac{1}{5}} \right) \cup \left( {3,\infty } \right)\].
Therefore, the solution of \[\left| {2x + 1} \right| < \left| {3x - 2} \right|\] is \[\left( { - \infty , - \dfrac{1}{2}} \right) \cup \left( { - \dfrac{1}{2},\dfrac{1}{5}} \right) \cup \left( {3,\infty } \right)\].

Note:
The solution range of inequality gives us each and every value of \[x\] which satisfies the equation. Here, one point to note is that square bracket \[\left[ {} \right]\] states that the end elements of the range will satisfy the given expression whereas the round bracket \[\left( {} \right)\] states that the end elements will not satisfy the given expression.