Question

Solve graphically: \[5x-6y+30=0;5x+4y-20=0\] also find the vertices of the triangle formed by above two lines and \[x-axis\]
A). \[(3,5),(4,2),(6,9)\]
B). \[(0,5),(-6,0),(4,0)\]
C). \[(0,2),(7,2),(0,4)\]
D). \[(2,3),(1,7),(3,9)\]

Answer 1

Hint: In this question first of all mark both the equation as equation one and equation two after that put the value of \[x=0\] and \[y=0\] one by one in both the equation then justify your answer with the help of graph and check which option is correct in the given options.

Complete step-by-step solution:
Algebra is a branch of mathematics that deals with symbols and the rules that govern their use. Elementary algebra refers to the most fundamental aspects of algebra, whereas Abstract Algebra or modern algebra refers to the more abstract types.
Linear equations are just another category of equations. Linear equations can be used to perform any linear calculations that require more than one variable. A linear equation in one variable has the conventional form of \[ax+b=0\]. \[x\] is a variable, and \[a,b\] are constants in this equation. A linear equation in two variables is written in the conventional form as \[ax+by=c\]. The variables \[x,y\] are variables, while the constants \[a,b\] and \[c\] are constants.A linear equation is a mathematical expression that has two variables. A constant can be present in this equation, which will be a linear combination of these two variables. Surprisingly, every linear equation plotted on a graph will always result in a straight line, therefore the name: linear equations.
A horizontal axis is typically referred to as the \[x-axis\] , while a vertical axis is referred to as the \[y-axis\] in a two-dimensional coordinate system.
In this question we have given two equations:
\[\Rightarrow 5x-6y+30=0\] and \[5x+4y-20=0\]
Write the equation in proper way we get:
 \[\Rightarrow 5x-6y=-30\] mark it as equation \[(1)\]
\[\Rightarrow 5x+4y=20\] mark it as equation \[(2)\]
Now if we put the value of \[y=0\] in equation \[(1)\]
\[\Rightarrow 5x-6\times 0=-30\]
\[\Rightarrow 5x=-30\]
\[\Rightarrow x=\dfrac{-30}{5}\]
\[\Rightarrow x=-6\]
Now put \[x=0\] in equation \[(1)\]
\[\Rightarrow 5\times 0-6y=-30\]
\[\Rightarrow -6y=-30\]
\[\Rightarrow y=\dfrac{-30}{-6}\]
\[\Rightarrow y=5\]
According to equation \[(1)\] on \[x-axis\] we have got: \[y=0,x=-6\]
Now if we put the value of \[y=0\] in equation \[(2)\]
\[\Rightarrow 5x+4\times 0=20\]
\[\Rightarrow 5x=20\]
\[\Rightarrow x=\dfrac{20}{5}\]
\[\Rightarrow x=4\]
Now put \[x=0\] in equation \[(2)\]
\[\Rightarrow 5\times 0+4y=20\]
\[\Rightarrow 4y=20\]
\[\Rightarrow y=\dfrac{20}{4}\]
\[\Rightarrow 4=5\]
According to equation \[(2)\] on \[x-axis\] we have got: \[y=0,x=\text{ }4\]
We can show it graphically:

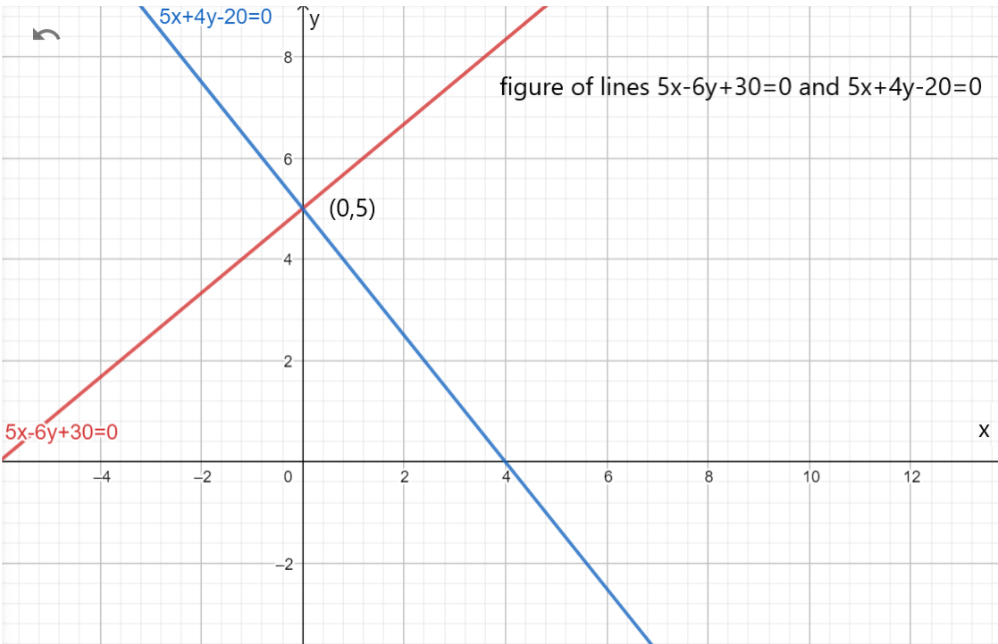
Hence we can conclude that option \[(B)\] is correct as the points are \[(0,5),(-6,0),(4,0)\].

Note: When the same number is added, subtracted, multiplied, or divided into both sides of a linear equation, the solution remains unchanged. The solution or root of a linear equation refers to the values of the variable that make the equation true. A linear equation with one or two variables has a straight line as its graph.