Question

Solve for the value of $x$ and $y$ if $2y-x=0$ and $10x+15y=105$.

Answer 1

Hint: For solving this problem as we have two linear equations in terms of two unknown variables. We will directly substitute the value of one of the variables in terms of another from one equation to another equation and then solve to find the value of unknown variables.

Complete step-by-step answer:
Given:
We have two linear equations $2y-x=0$ , $10x+15y=105$ and we have to find the value of $x$ and $y$.
Now, the given equations are:
$\begin{align}
  & 2y-x=0...........\left( 1 \right) \\
 & 10x+15y=105............\left( 2 \right) \\
\end{align}$
Now, from the equation (1) we can substitute the value of $x=2y$ into equation (2). Then,
$\begin{align}
  & 10x+15y=105 \\
 & \Rightarrow 10\times 2y+15y=105 \\
 & \Rightarrow 20y+15y=105 \\
 & \Rightarrow 35y=105 \\
 & \Rightarrow y=3 \\
\end{align}$
Now, from the above equation substituting the value of $y=3$ in the equation (1). Then,
$\begin{align}
  & x-2y=0 \\
 & \Rightarrow x-6=0 \\
 & \Rightarrow x=6 \\
\end{align}$
Now, from the above results we can say that if $2y-x=0$ and $10x+15y=105$ then, the value of $x=6$ and value of $y=3$ . For more clarity, we can also plot both given equations on the x-y plane and verify whether they are intersecting at point (6,3) or not. The plot is shown below:

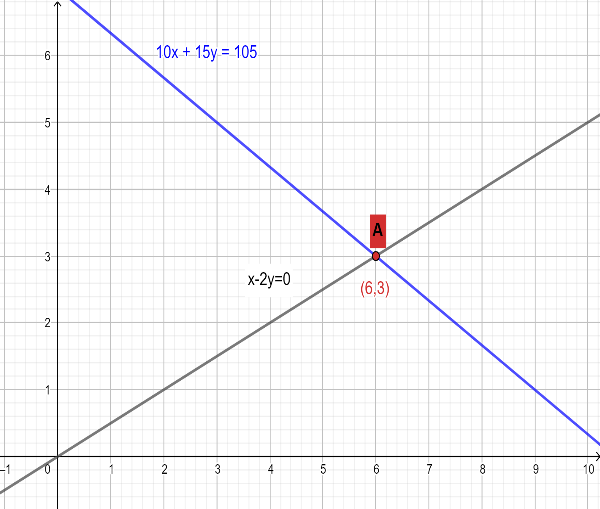
Now, from the above figure, we can verify that the given two equations of straight lines will intersect at the point whose $x$ coordinate will be $x=6$ and $y$ coordinate will be $y=3$ .
Hence, if $2y-x=0$ and $10x+15y=105$ then, the value of $x=6$ and value of $y=3$.

Note: Here, the student should simply do the substitution correctly and though the problem is very easy, we should avoid calculation mistakes while solving. Moreover, in such questions once we solve the equations then, we should verify it from graphs for better understanding.