
How do you solve $\dfrac{1}{2}a + \dfrac{1}{3}b = 8$, $\dfrac{3}{2}a - \dfrac{4}{3}b = - 4$?
Answer
546.6k+ views
Hint: First we have to make the first linear equation in Slope-intercept form and then calculate the value of $y$ for any two arbitrary values of $x$. Next make a table of these values of $x$ and $y$. Next plot the obtained points on the graph paper and draw a line passing through these points. Now repeat the process with the second equation and determine the solution of the given system of equations using the graph obtained.
Formula used:
Slope Intercept of a line:
The equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.
Complete step by step solution:
First, we have to move $\dfrac{1}{2}a$to right side of the equation, $\dfrac{1}{2}a + \dfrac{1}{3}b = 8$. Thus, subtracting $\dfrac{1}{2}a$ to both sides of the equation.
$ \Rightarrow \dfrac{1}{3}b = 8 - \dfrac{1}{2}a$
Now, multiply both sides of the equation by $3$.
$ \Rightarrow b = 24 - \dfrac{3}{2}a$…(i)
Now, we have to calculate the value of $b$ for any two arbitrary values of $a$. Thus, finding the value of $y$ when $a = 4$ and $a = 8$.
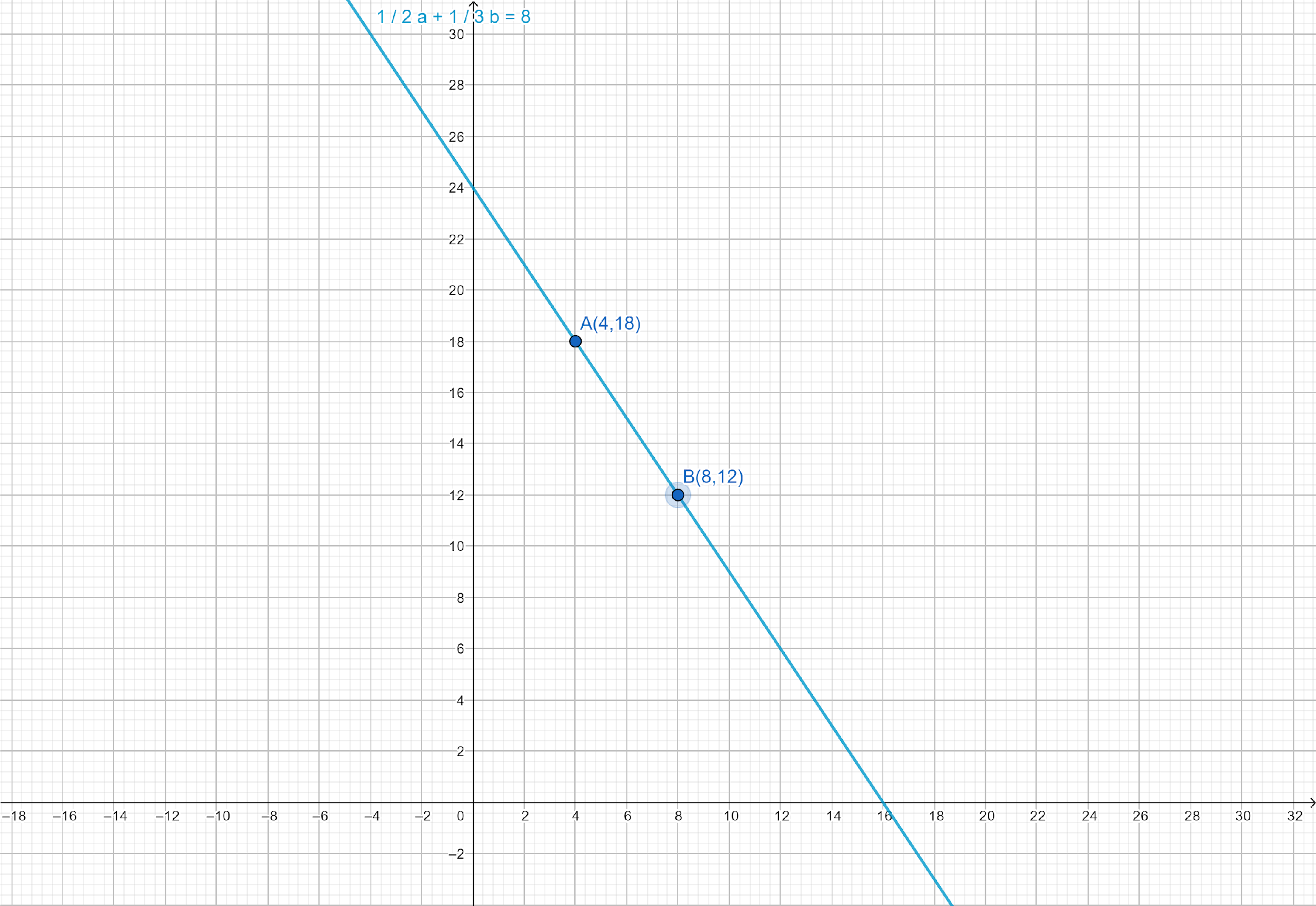
When $a = 4$, $b = 24 - \dfrac{3}{2} \times 4 = 18$
When $a = 8$, $b = 24 - \dfrac{3}{2} \times 8 = 12$
Now we have to make a table of these values of $a$ and $b$.
Now we have to plot the points $A\left( {4,18} \right)$ and $B\left( {8,12} \right)$ on the graph paper and draw a line passing through $A$ and $B$, we get the graph of equation $\dfrac{1}{2}a + \dfrac{1}{3}b = 8$.
Now we have to make the second equation in Slope-intercept form. Thus, subtracting $\dfrac{3}{2}a$ to both sides of the equation.
$ \Rightarrow - \dfrac{4}{3}b = - 4 - \dfrac{3}{2}a$
Now, multiply both sides of the equation by $ - \dfrac{3}{4}$.
$ \Rightarrow b = 3 + \dfrac{9}{8}a$…(ii)
Now, we have to calculate the value of $b$ for any two arbitrary value of $a$. Thus, finding the value of $y$ when $a = 0$ and $a = 16$.
When $a = 0$, $b = 3 + \dfrac{9}{8} \times 0 = 3$
When $a = 16$, $b = 3 + \dfrac{9}{8} \times 16 = 21$
Now we have to make a table of these values of $a$ and $b$.
Now we have to plot the points $C\left( {0,3} \right)$ and $D\left( {16,21} \right)$ on the graph paper and draw a line passing through $C$ and $D$, we obtain the graph of the equation $\dfrac{3}{2}a - \dfrac{4}{3}b = - 4$.
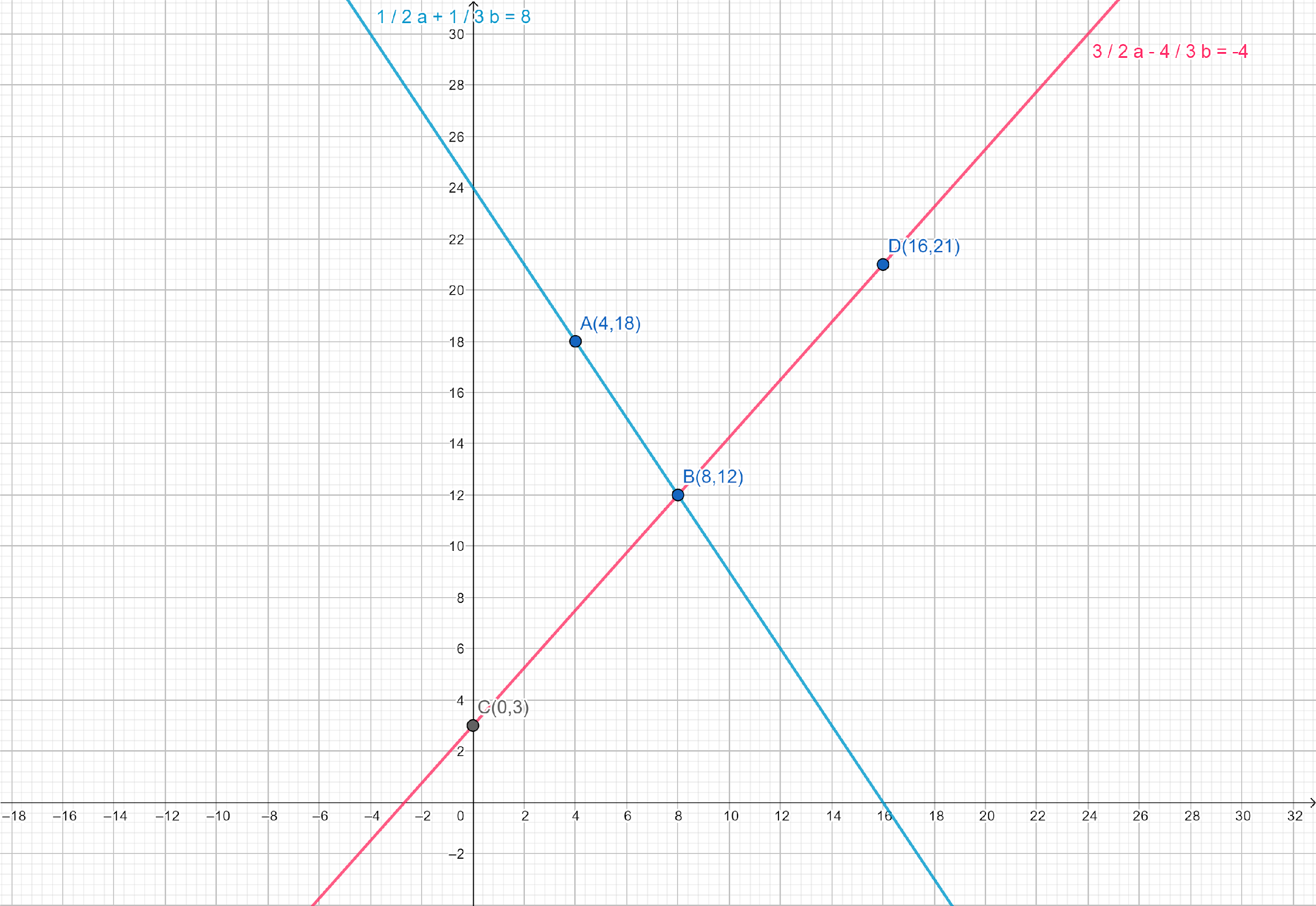
Clearly, two lines intersect at point $B\left( {8,12} \right)$.
Final solution: Hence, $a = 8$ and $b = 12$ is the solution of the given system.
Note: We can directly find the solution of a given system by Method of Elimination.
Method of Elimination:
In this method, we eliminate one of the two variables to obtain an equation in one variable which can be easily solved. Putting the value of this variable in any one of the given equations, the value of another variable can be obtained.
Step by step solution:
The given system of equations is
$\dfrac{1}{2}a + \dfrac{1}{3}b = 8$
$\dfrac{3}{2}a - \dfrac{4}{3}b = - 4$
We can eliminate the $b$ variable by equating the right side of equations (i) and (ii).
$ \Rightarrow 24 - \dfrac{3}{2}a = 3 + \dfrac{9}{8}a$
Multiply both sides of equation by $8$, we get
$ \Rightarrow 192 - 12a = 24 + 9a$
It can be further simplified as
$ \Rightarrow 9a + 12a = 192 - 24$
$ \Rightarrow 21a = 168$
Now, divide both sides of the equation by $21$.
$ \Rightarrow a = 8$
Now, substitute the value of $a$ in equation (i) and find the value of $b$.
$ \Rightarrow b = 24 - \dfrac{3}{2} \times 8$
$ \Rightarrow b = 12$
Final solution: Hence, $a = 8$ and $b = 12$ is the solution of the given system
Formula used:
Slope Intercept of a line:
The equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.
Complete step by step solution:
First, we have to move $\dfrac{1}{2}a$to right side of the equation, $\dfrac{1}{2}a + \dfrac{1}{3}b = 8$. Thus, subtracting $\dfrac{1}{2}a$ to both sides of the equation.
$ \Rightarrow \dfrac{1}{3}b = 8 - \dfrac{1}{2}a$
Now, multiply both sides of the equation by $3$.
$ \Rightarrow b = 24 - \dfrac{3}{2}a$…(i)
Now, we have to calculate the value of $b$ for any two arbitrary values of $a$. Thus, finding the value of $y$ when $a = 4$ and $a = 8$.
When $a = 4$, $b = 24 - \dfrac{3}{2} \times 4 = 18$
When $a = 8$, $b = 24 - \dfrac{3}{2} \times 8 = 12$
Now we have to make a table of these values of $a$ and $b$.
| $a$ | $4$ | $8$ |
| $b$ | $18$ | $12$ |
Now we have to plot the points $A\left( {4,18} \right)$ and $B\left( {8,12} \right)$ on the graph paper and draw a line passing through $A$ and $B$, we get the graph of equation $\dfrac{1}{2}a + \dfrac{1}{3}b = 8$.

Now we have to make the second equation in Slope-intercept form. Thus, subtracting $\dfrac{3}{2}a$ to both sides of the equation.
$ \Rightarrow - \dfrac{4}{3}b = - 4 - \dfrac{3}{2}a$
Now, multiply both sides of the equation by $ - \dfrac{3}{4}$.
$ \Rightarrow b = 3 + \dfrac{9}{8}a$…(ii)
Now, we have to calculate the value of $b$ for any two arbitrary value of $a$. Thus, finding the value of $y$ when $a = 0$ and $a = 16$.
When $a = 0$, $b = 3 + \dfrac{9}{8} \times 0 = 3$
When $a = 16$, $b = 3 + \dfrac{9}{8} \times 16 = 21$
Now we have to make a table of these values of $a$ and $b$.
| $a$ | $0$ | $16$ |
| $b$ | $3$ | $21$ |
Now we have to plot the points $C\left( {0,3} \right)$ and $D\left( {16,21} \right)$ on the graph paper and draw a line passing through $C$ and $D$, we obtain the graph of the equation $\dfrac{3}{2}a - \dfrac{4}{3}b = - 4$.

Clearly, two lines intersect at point $B\left( {8,12} \right)$.
Final solution: Hence, $a = 8$ and $b = 12$ is the solution of the given system.
Note: We can directly find the solution of a given system by Method of Elimination.
Method of Elimination:
In this method, we eliminate one of the two variables to obtain an equation in one variable which can be easily solved. Putting the value of this variable in any one of the given equations, the value of another variable can be obtained.
Step by step solution:
The given system of equations is
$\dfrac{1}{2}a + \dfrac{1}{3}b = 8$
$\dfrac{3}{2}a - \dfrac{4}{3}b = - 4$
We can eliminate the $b$ variable by equating the right side of equations (i) and (ii).
$ \Rightarrow 24 - \dfrac{3}{2}a = 3 + \dfrac{9}{8}a$
Multiply both sides of equation by $8$, we get
$ \Rightarrow 192 - 12a = 24 + 9a$
It can be further simplified as
$ \Rightarrow 9a + 12a = 192 - 24$
$ \Rightarrow 21a = 168$
Now, divide both sides of the equation by $21$.
$ \Rightarrow a = 8$
Now, substitute the value of $a$ in equation (i) and find the value of $b$.
$ \Rightarrow b = 24 - \dfrac{3}{2} \times 8$
$ \Rightarrow b = 12$
Final solution: Hence, $a = 8$ and $b = 12$ is the solution of the given system
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

The draft of the Preamble of the Indian Constitution class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

Who gave "Inqilab Zindabad" slogan?

Who was Subhash Chandra Bose Why was he called Net class 10 english CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE




