Question

How do you solve $\cos x+1=0$ and find all solutions in the interval $0\le x<360$?

Answer 1

Hint: We explain the function $\cos x+1=0$. We express the inverse function of cos in the form of $\arccos \left( x \right)={{\cos }^{-1}}x$. We draw the graph of $\cos x$ and the line $y=-1$ to find the intersection point as the solution for the interval $0\le x<360$.

Complete step by step answer:
The given expression is the inverse function of trigonometric ratio cos.
If \[{{\cos }^{-1}}x=\alpha \] then we can say $\cos \alpha =x$.
Each of the trigonometric functions is periodic in the real part of its argument, running through all its values twice in each interval of $2\pi $.
The general solution for that value where $\cos \alpha =x$ will be $2n\pi \pm \alpha ,n\in \mathbb{Z}$.
But for $\arccos \left( x \right)$, we won’t find the general solution. We use the principal value. For ratio cos we have $0\le \arccos \left( x \right)\le \pi $.
Now we take the function as $y=\cos x=-1$. The graph of the function $y=\cos x$ is

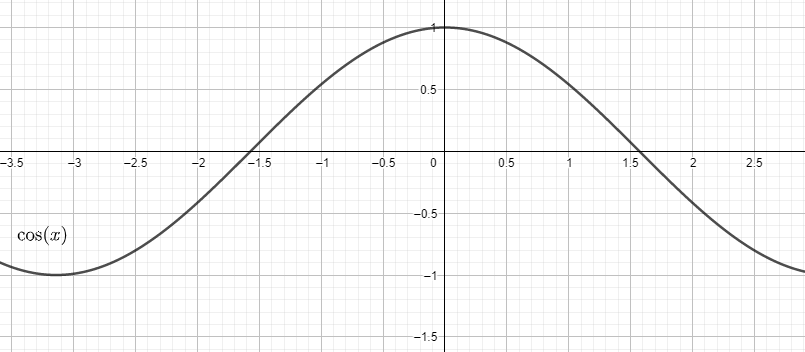
Let the angle be $\theta $ for which $\arccos \left( x \right)={{\cos }^{-1}}x=\theta $. This gives $\cos \theta =-1$.
We know that $\cos \theta =-1=\cos \left( \pi \right)$ which gives $\theta =\pi $. For this we take the line of $y=-1$ and see the intersection of the line with the graph $\arccos \left( x \right)$.
The general solution of the function $\cos x+1=0$ is $2n\pi \pm \alpha ,n\in \mathbb{Z}$

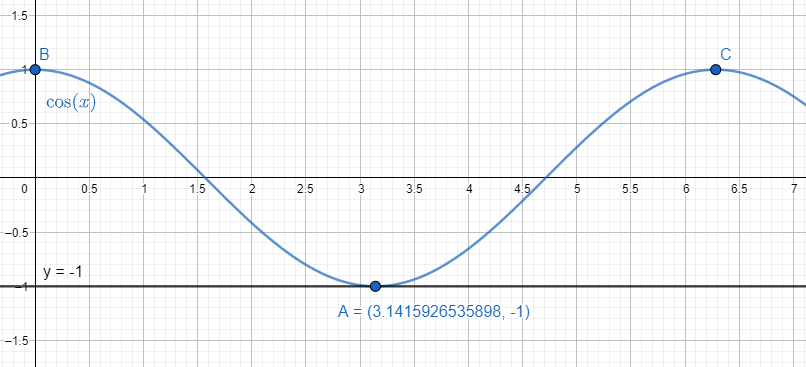
We get the value of y coordinates as $\pi $. The points B and C are the points $B\equiv \left( 0,1 \right)$ and $C\equiv \left( 2\pi ,1 \right)$. In the interval of $0\le x<360$, the only intersection of the curve $y=\cos x$ and the line $y=-1$ is point $A\equiv \left( \pi ,-1 \right)$.
The general solution of the function $\cos x+1=0$ is $2n\pi \pm \pi ,n\in \mathbb{Z}$. The simplified solution for $\cos x+1=0$ is $\left( 2n\pm 1 \right)\pi ,n\in \mathbb{Z}$.

Note:
If we are finding an $\arccos \left( x \right)$ of a positive value, the answer is between $0\le \arccos \left( x \right)\le \dfrac{\pi }{2}$. If we are finding the $\arccos \left( x \right)$ of a negative value, the answer is between $\dfrac{\pi }{2}\le \arccos \left( x \right)\le \pi $.