Question

How do you solve and graph the solution set of \[\left| 2x-1 \right|\le 2\]?

Answer 1

Hint: The given question is inequality of modulus, to solve it we should know the properties of modulus. As the question has an inequality, we will get a range of solutions rather than a single value of solution. We should know the property of modulus which states that, \[\left| x \right|\le a\] can also be expressed as \[-a\le x\le a\]. We should also know the property of inequalities that states that adding or subtracting and multiplying by a positive quantity will not change the inequality sign.

Complete step-by-step solution:
We are given the equation \[\left| 2x-1 \right|\le 2\]. We know the property of modulus that states \[\left| x \right|\le a\] can also be expressed as \[-a\le x\le a\]. Using this property, we get
\[\begin{align}
  & \Rightarrow \left| 2x-1 \right|\le 2 \\
 & \Rightarrow -2\le 2x-1\le 2 \\
\end{align}\]
Adding 1 on all sides of the above inequality, we get
\[\Rightarrow -1\le 2x\le 3\]
We divide the above inequality by 2, as 2 is a positive quantity dividing by it will not change the inequality sign. By doing this, we get
\[\Rightarrow \dfrac{-1}{2}\le \dfrac{2x}{2}\le \dfrac{3}{2}\]
 By cancelling out the common factor, we get the inequality as
\[\Rightarrow \dfrac{-1}{2}\le x\le \dfrac{3}{2}\]
Thus, the above inequality gives the range as
\[\Rightarrow x\in \left[ \dfrac{-1}{2},\dfrac{3}{2} \right]\]
We can graph the inequality as shown below,

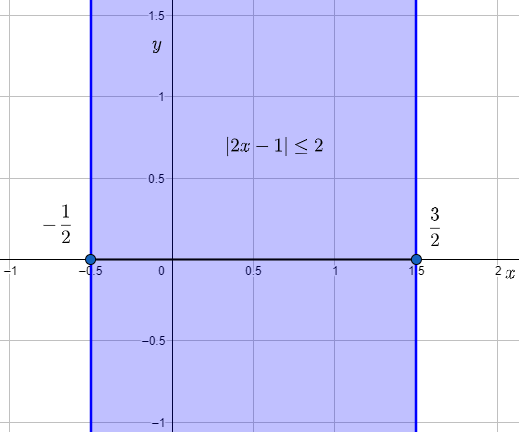
Since the values of x are inclusive, we have used solid lines at points.

Note: While solving the questions based on inequality, we should be careful that whether performing an operation will change the inequality or not. The inequality sign will not change by adding or subtracting, also by multiplying or dividing a positive quantity, but the sign will change if a negative quantity is multiplied or divided to both sides. We should also know the properties of modulus function.