Question

How do you solve and graph the compound inequality $ 2 < x <7 $ and $ 2x > 10 $ ?

Answer 1

Hint: We try to take points which have x coordinates that satisfies $ 2 < x < 7 $ and
$ 2x>10 $ . There is no restriction on the y coordinates. Based on the points we try to find the space or region in the 2-D plane which satisfies $ 2 < x < 7 $ and $ 2x>10 $ . We have two inequalities to solve to get the required interval.

Complete step by step solution:
Simplifying the inequation $ 2 < x < 7 $ , we get the interval of $ x\in \left( 2,7 \right) $ .
Now we solve the inequation $ 2 x > 10 $ .
We can solve the inequation treating them as equations for the operations like addition and subtraction. In case of multiplication and division we need to watch out for the negative values as that changes the inequality sign.
We divide both side of $ 2x>10 $ with positive number 2 and get
 $ \begin{align}
  & \dfrac{2x}{2}>\dfrac{10}{2} \\
 & \Rightarrow x>5 \\
\end{align} $
The interval is $ x\in \left( 5,\infty \right) $ .
We need to take the combined result of $ x\in \left( 2,7 \right) $ and $ x\in \left( 5,\infty \right) $ .
The final solution gives $ x\in \left( 5,7 \right) $ .

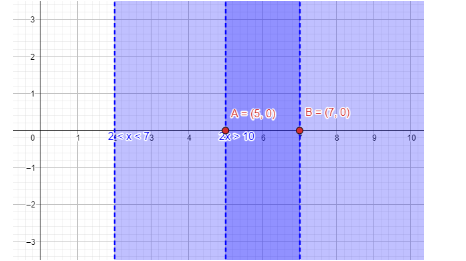
Note: We can also express the inequality as the interval system where $ 2x>10 $ defines that $ x>5 $ . The interval for the y coordinates will be anything which can be defined as $ y\in \left( -\infty ,\infty \right) $ . We also need to remember that the boundary points will not be considered as the solution for the inequations.