Question

How do you solve and graph \[\left| {\dfrac{{3h + 1}}{2}} \right| < 8\] ?

Answer 1

Hint:Here in this question, we have to plot a graph for the absolute value. Usually while plotting the graph, we plot x axis versus y- axis. But here in this question we have only one variable and we have greater than and less than inequality. For this variable we have to plot the graph. Hence, we get a line. We cannot specify a particular point.

Complete step by step explanation:
The graph is generally plotted x- axis versus y -axis. When we have two variables then we plot a two-dimensional graph. Here in this question, we have only one variable but this also a two-dimensional graph. The absolute value function takes any term and transforms it to its non-negative form. Therefore, we must solve the term within the absolute value function for both its negative and positive equivalent
Consider the given absolute value
\[\left| {\dfrac{{3h + 1}}{2}} \right| < 8\]
It can be written as
\[ \Rightarrow \,\,\, - 8 < \dfrac{{3h + 1}}{2} < 8\]
multiply each segment of the system of inequalities by 2 to eliminate the fraction while keeping the system balanced.
\[ \Rightarrow \,\,\, - 16 < 3h + 1 < 16\]
subtract 1 from each segment to isolate the h term.
\[ \Rightarrow \,\,\, - 16 - 1 < 3h + 1 - 1 < 16 - 1\]
On simplification, we get
\[ \Rightarrow \,\,\, - 17 < 3h < 15\]
divide each segment by 3 to solve for h.
\[ \Rightarrow \,\,\, - \dfrac{{17}}{3} < \dfrac{{3h}}{3} < \dfrac{{15}}{3}\]
On simplification, we get
\[ \Rightarrow \,\,\, - \dfrac{{17}}{3} < h < 5\]
or
\[ \Rightarrow \,\,\, - \dfrac{{17}}{3} < h\] and \[h < 5\].
The graph for the given equation \[\left| {\dfrac{{3h + 1}}{2}} \right| < 8\] is as shown below.

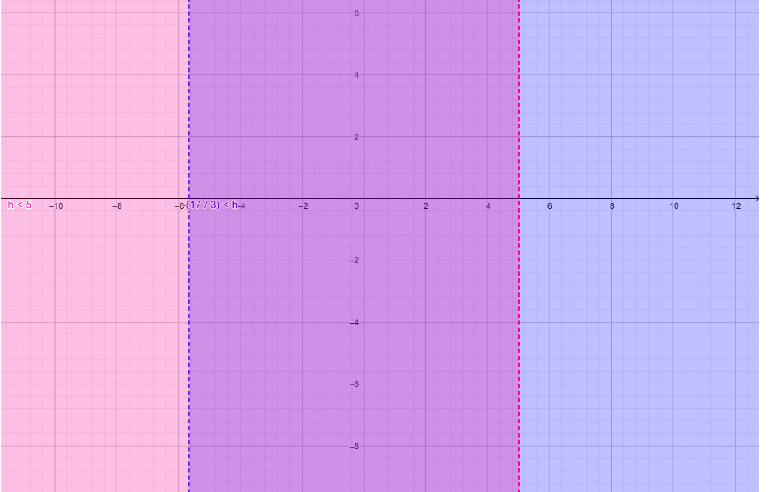
Note: The graph is plotted against the two axes namely X-axis and Y-axis. If we know the value of one, we can find the other by using the equation of the graph. This graph is two dimensional because they have mentioned only two axes. The value of y can range, it does not have particular value. Because the inequality has greater than and less than symbols.