Question

How do you solve and graph $ 4 < y + 2 < - 3(y - 2) + 24 $ ?

Answer 1

Hint: Take out all the like terms to one side and all the alike terms to the other side. Take out all the common terms. Reduce the terms on the both sides until they cannot be reduced any further if possible. Then finally evaluate the value of the unknown variable. Solve both the inequalities separately.

Complete step-by-step answer:
First we will start off by evaluating the inequality $ 4 < y + 2 $
Now we subtract $ 2 $ from both the sides so we get,
 $ 4 - 2 < y + 2 - 2 $
 $ 2 < y $
Now we will evaluate the second inequality that is $ y + 2 < - 3(y - 2) + 24 $ .
We will first open the brackets and simplify the terms.
 $ y + 2 < - 3(y - 2) + 24 $
 $ y + 2 < - 3y + 6 + 24 $
 $ y + 2 < - 3y + 30 $
Now we will add $ (3y - 2) $ to both the sides.
 $ y + 2 + (3y - 2) < - 3y + 30 + (3y - 2) $
 $ 4y < 28 $
Divide both the sides by $ 4 $ .
 $ y < 7 $
Now if we recombine the equations, we will get,
 $ \Rightarrow 2 < y < 7 $
Now we will plot the graph.
Now take
 $ \Rightarrow 2 < y $ or $ 4 < y + 2 $ .

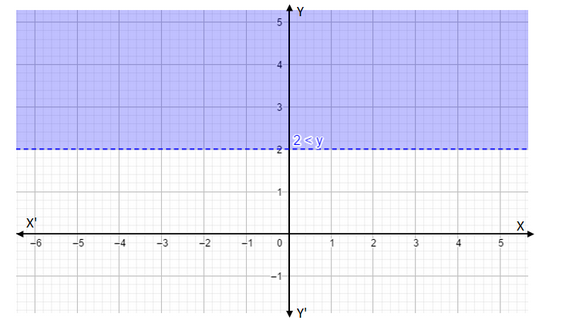
In the above graph the shaded region is the solution of $ 2 < y $ Also if we take a point lies on the line $ y = 2 $ the inequality $ 4 < y + 2 $ doesn't satisfy.
Now take
 $ \Rightarrow y < 7 $ or $ y + 2 < - 3(y - 2) + 24 $

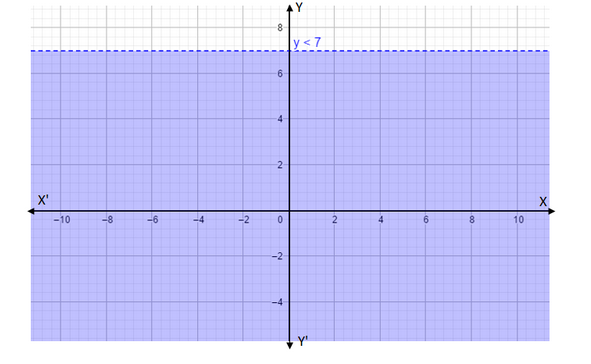
In the above graph the shaded region is the solution of $ y < 7 $ Also if we take a point lies on the line $ y = 7 $ the inequality $ y + 2 < - 3(y - 2) + 24 $ don’t satisfy

Note: When drawing the graph of the inequality of $ 2 < y $ and $ y < 7 $ we consider $ y = 2 $ and $ y = 7 $ . As we can see, it has two parallel lines to ‘x’-axis. In the question we have simple linear inequality with one variable and we follow the same procedure for these kinds of problems.